题目内容
【题目】阅读材料,回答下列问题:
阿尔花拉子米(约780~约850),著名阿拉伯数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”.他利用正方形图形巧妙解出了一元二次方程x2+2x﹣35=0的一个解.
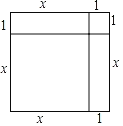
将边长为x的正方形和边长为1的正方形,外加两个长方形,长为x,宽为1,拼合在一起面积就是x2+2×1+1×1,即x2+2x+1,而由原方程x2+2x﹣35=0变形得x2+2x+1=35+1,即右边边长为x+1的正方形面积为36.所以(x+1)2=36,则x=5.
(1)上述求解过程中所用的方法与下列哪种方法是一致的 .
A.直接开平方法 B.公式法
C.配方法 D.因式分解法
(2)所用的数学思想方法是 .
A.分类讨论思想 B.数形结合思想 C.转化思想
(3)运用上述方法构造出符合方程x2+4x﹣5=0的一个正根的正方形.
【答案】(1)C;(2)B;(3)x=1,见解析.
【解析】
(1)由阅读材料所用方法可知答案;
(2)结合图形来解题,故答案易得;
(3)构造出边长为x+2的正方形,其面积为9,则x=1为方程的一个正根.
(1)由阅读材料可知所用方法为配方法.
故答案为:C.
(2)所用的思想方法为数形结合思想.
故答案为:B.
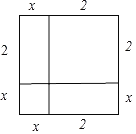
(3)将边长为x的正方形和边长为2的正方形,外加两个长方形,长为x,宽为2,拼合在一起面积就是x2+2×2×x+2×2,即x2+4x+4,
而由原方程x2+4x﹣5=0变形得x2+4x+4=9,即图中边长为x+2的正方形面积为9.
所以(x+2)2=9,x+2=3
则x=1.

练习册系列答案
相关题目