题目内容
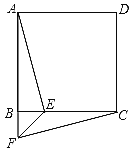
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点P以
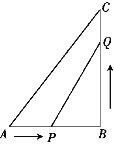
,动点P以![]() 的速度从A点出发,沿
的速度从A点出发,沿![]() 向C点移动,同时动点Q以
向C点移动,同时动点Q以![]() 的速度从点C出发,沿
的速度从点C出发,沿![]() 向点B移动,设P、Q两点移动的时间为t秒
向点B移动,设P、Q两点移动的时间为t秒![]() .
.
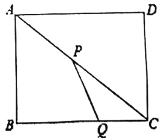
(1)t为多少时,以P、Q、C为顶点的三角形与![]() 相似?
相似?
(2)在P、Q两点移动过程中,四边形![]() 与
与![]() 的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
【答案】(1)t为![]() 或
或![]() 时,以P、Q、C为顶点的三角形与
时,以P、Q、C为顶点的三角形与![]() 相似;(2)四边形
相似;(2)四边形![]() 与
与![]() 的面积不能相等,理由见解析.
的面积不能相等,理由见解析.
【解析】
(1)先利用勾股定理计算出AC=10,由于∠PCQ=∠ACB,根据三角形相似的判定,当∠PQC=∠B时可判断CQP∽△CBA,利用相似比得到![]() ;当∠PQC=∠BAC时可判断△CQP∽△CAB,利用相似比得到
;当∠PQC=∠BAC时可判断△CQP∽△CAB,利用相似比得到![]() ,然后分别解方程求出t的值即可;
,然后分别解方程求出t的值即可;
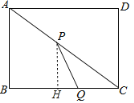
(2)作PQ⊥BC于H,如图,先证明△CPH∽△CAB,利用相似比可得到PH=![]() ,再利用四边形ABQP与△CPQ的面积相等得到S△ABC=2S△CPQ,利用三角形面积公式得到2
,再利用四边形ABQP与△CPQ的面积相等得到S△ABC=2S△CPQ,利用三角形面积公式得到2![]() 68,然后解关于t的方程可判断四边形ABQP与△CPQ的面积能否相等.
68,然后解关于t的方程可判断四边形ABQP与△CPQ的面积能否相等.
(1)在R![]() 中,
中,![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ;
;
∴t为![]() 或
或时,以P、Q、C为顶点的三角形与
![]() 相似;
相似;
(2)四边形![]() 与
与![]() 的面积不能相等.
的面积不能相等.
理由如下:
作![]() 于H,如图,
于H,如图,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
当四边形![]() 与
与![]() 的面积相等时,
的面积相等时,
![]() ,即
,即![]() ,
,
∴![]() ,
,
整理得![]() ,此时方程无实数解,
,此时方程无实数解,
∴四边形![]() 与
与![]() 的面积不能相等.
的面积不能相等.

【题目】九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);
②运动服的进价是 元/件;当售价是 元/件时,月销利润最大,最大利润是 元.
(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.