题目内容
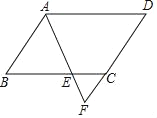
【题目】如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.
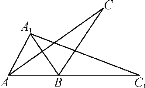
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
【答案】(1)60°(2)证明见解析
【解析】
(1)∠CBC1即为旋转角,其中∠ABC=120°,所以,∠CBC1=180°﹣∠ABC;
(2)由题意知,△ABC≌△A1BC1,易证△A1AB是等边三角形,得到AA1∥BC,继而得出结论;
(1)∵∠ABC=120°,∴∠CBC1=180°﹣∠ABC=180°﹣120°=60°,∴旋转角为60°;
(2)由题意可知:△ABC≌△A1BC1,∴A1B=AB,∠C=∠C1,由(1)知,∠ABA1=60°,∴△A1AB是等边三角形,∴∠BAA1=60°,∴∠BAA1=∠CBC1,∴AA1∥BC(同位角相等,两直线平行),∴∠A1AC=∠C(两直线平行,内错角相等),∴∠A1AC=∠C1.

【题目】九年级孟老师数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);
②运动服的进价是 元/件;当售价是 元/件时,月销利润最大,最大利润是 元.
(2)由于某种原因,该商品进价降低了m元/件(m>0),商家规定该运动服售价不得低于150元/件,该商店在今后的售价中,月销售量与售价仍满足(1)中的函数关系式,若月销售量最大利润是12000元,求m的值.