��Ŀ����
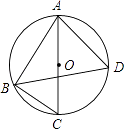
����Ŀ����ͼ����֪�ı���ABCD�У���B=60������AB=BC=8cm������P��Qͬʱ��A��B����������ֱ���AB��BC���������˶������е�P�˶����ٶ���ÿ��1cm����Q�˶����ٶ���ÿ��2cm������Q�����Cʱ��P��Q���㶼ֹͣ�˶������˶�ʱ��Ϊt�룮
����������⣺
��1��AP=�� ����BP=�� ����BQ=�� �������ú�t�Ĵ���ʽ��ʾ��t��4��
��2������Q�����Cʱ��PQ��AB��λ�ù�ϵ��Σ���˵�����ɣ�
��3���ڵ�P���Q���˶������У���BPQ�Ƿ��ܳ�Ϊ�ȱ������Σ����ܣ������t�������ܣ���˵�����ɣ�

���𰸡���1��t��8��t��2t����2��PQ��AB�����ɼ���������3����BPQ�ܳ�Ϊ�ȱ������Σ�t=![]() ��
��
��������
��1�����ݵ�P��Q���˶��ٶȽ����
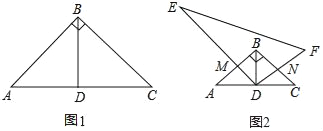
��2������AC���õ���ABCΪ�ȱ������������ݵ��������ε����ߺ�һ֤����
��3�����ݵȱ������ε��ж������г��������ⷽ�̼�����
��1��������ã�AP=t��BP=8��t��BQ=2t��
�ʴ�Ϊ��t��8��t��2t��
��2��PQ��AB���������£�
����AC��
�ߡ�B=60����AB=BC�����ABCΪ�ȱ������Σ�
�ߵ�Q�����Cʱ��BQ=BC=8cm��AP=4����PΪAB���е㣬��PQ��AB��
��3����BPQ�ܳ�Ϊ�ȱ������Σ�
�ߡ�B=60�����൱BP=BQʱ����BPQ�ܳ�Ϊ�ȱ������Σ���ʱ��8��t=2t����ã�![]() ��
��

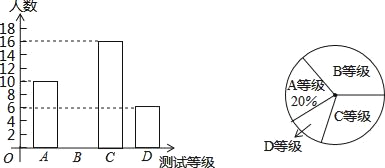
����Ŀ��Ϊ�˽�ij�о��꼶ѧ��ѧҵ���������ɼ����ִ��������ȡ����ѧ���������ɼ����зֶ�ͳ�����£�
ѧҵ���������ɼ��������Σ�ͳ�Ʊ� | ||
������ | �������ˣ� | Ƶ�� |
A | 48 | 0.2 |
B | a | 0.25 |
C | 84 | 0.35 |
D | 36 | b |
E | 12 | 0.05 |
������Ϊ����A��50�֣�B��49��45�֣�C��44��40�֣�D��39��30�֣�E��29��0�֣� 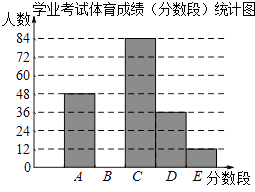
���������ṩ����Ϣ���ش��������⣺
��1����ͳ�Ʊ��У�a��ֵΪ �� b��ֵΪ ��
��2����ͳ��ͼ������������ܰ��ʾ����ͼʱ��������0.5�������ϵĺ�ɫǩ�ֱ�Ϳ�ڣ���
��3����ͬѧ˵�����ҵ������ɼ��Ǵ˴γ��������������ݵ���λ���������ʣ���ͬѧ�������ɼ�Ӧ��ʲô�������ڣ�������Ӧ�����ε���ĸ��
��4������ѳɼ���40�����ϣ���40�֣���Ϊ���㣬��ô���н���10440�����꼶ѧ���������ɼ�Ϊ�����ѧ������Լ�ж�������