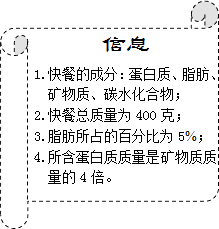
题目内容
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
【答案】(1)t=![]() ;(2)t=
;(2)t=![]() ;
;
【解析】
(1)设存在点P,使得PA=PB,此时PA=PB=2t,PC=4-2t,根据勾股定理列方程即可得到结论;
(2)当点P在∠CAB的平分线上时,如图,过点P作PE⊥AB于点E,此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,根据勾股定理列方程即可得到结论.
(1)设存在点P,使得PA=PB,此时PA=PB=2t,
在Rt△ABC中,AC=![]() =
=![]() =4,PC=4–2t,
=4,PC=4–2t,
在Rt△PCB中,PC2+CB2=PB2,即:(4–2t)2+32=(2t)2,
解得t=![]() ,
,
∴当t=![]() 时,PA=PB;
时,PA=PB;
(2)当点P在∠BAC的平分线上时,如图,过点P作PE⊥AB于点E,
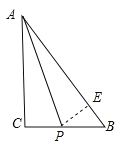
此时BP=7–2t,PE=PC=2t–4,BE=5–4=1,
在Rt△BEP中,PE2+BE2=BP2,
即:(2t–4)2+12=(7–2t)2,解得t=![]() ,
,
∴当t=![]() 时,P在∠BAC的平分线上.
时,P在∠BAC的平分线上.

练习册系列答案
相关题目