Question

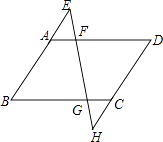
【题目】如图，在锐角三角形ABC中，∠BAC=60°，BF，CE为高，点D为BC的中点，连接EF，ED，FD，有下列四个结论：①ED=FD；②∠ABC=60°时，EF∥BC；③BF=2AF；④AF：AB=AE：AC．其中正确的个数有（　　）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】C

【解析】

①由BF、CE为高，D为BC的中点，根据直角三角形斜边上的中线等于斜边的一半，即可证得FD=ED；

②由两角对应相等，易证得△AEF∽△ABC，然后由∠BAC=60°与∠ABC=60°，可得△ABC是等边三角形，则易得∠AEF=∠ABC=60°，即可得EF∥BC；

③根据锐角三角函数的定义，可得③错误；

④可证△ABF∽△ACE，可得结论．

①∵BF、CE为高，

∴∠BEC=∠BFC=90°，

∵D为BC的中点，

∴FD=ED，

故①正确；

②∵BF、CE为高，

∴∠BFA=∠CEA=90°，

∵∠A=∠A，

∴△BFA∽△CEA，

∵∠BAC=60°，∠ABC=60°，

∴△ABC是等边三角形，

∴△AEF也是等边三角形，

∴∠AEF=∠ABC=60°，

∴EF∥BC，

故②正确；

③∵∠ABC=60°，

tan60°=，

∴BF=AF，

故③错误；

④∵∠AFB=∠AEC=90°，∠A=∠A，

∴△ABF∽△ACE，

得AF：AB=AE：AC．

故④正确；

本题正确的个数有3个：①②④；

故选C．