题目内容
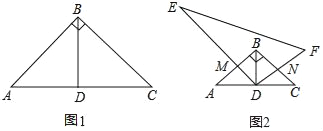
【题目】特例探究:如图①,已知在△ABC中,AB=BC,∠ABC=90°,D为AC边的中点,连接BD,判断△ABD是什么三角形,并说明理由.
归纳证明:如图②,已知在△ABC中,AB=BC,∠ABC=90°,D为AC边的中点,连接BD,把Rt△DEF的直角顶点D放在AC的中点上,DE交AB于M,DF交BC于N.证明:DM=DN.
拓展应用:在图②,AC=4,其他条件都不发生变化,请直接写出Rt△DEF与△ABC的重叠部分的面积.
【答案】特例探究:△ABD是等腰直角三角形,理由见解析;归纳证明:证明见解析;拓展应用:2.
【解析】
特例探究:根据等腰直角三角形的性质和三线合一,直接证得△ABD是等腰直角三角形即可;
归纳证明:证得△DMA≌△DNB(ASA),即可得出答案;
拓展应用:由归纳证明可知△DMA≌△DNB(ASA),同理可得△BDM≌△DCN(ASA),由此得出Rt△DEF与△ABC的重叠部分(四边形DMBN的面积是△ABC面积的一半,即可得出结论.
特例探究:△ABD是等腰直角三角形.理由如下:
∵AB=BC,∠ABC=90°,∴△ABC为等腰直角三角形.
∵D为AC边的中点,∴BD⊥AC,AD=CD=![]() AC,BD=
AC,BD=![]() AC,∴AD=BD,∴△ABD是等腰直角三角形.
AC,∴AD=BD,∴△ABD是等腰直角三角形.
归纳证明:∵AB=CB,∴∠A=∠C=45°.
∵D是AC的中点,∴DA=DC=BD,∠DBN=45°,BD⊥AC,∴∠ADB=∠ADM+∠BDM=90°,∴∠A=∠DBN.
∵∠EDF=90°,∴∠BDN+∠BDM=90°,∴∠ADM=∠BDN.
在△DMA和△DBN中,∵∠ADM=∠BDN,AD=BD,∠A=∠DBN,∴△DMA≌△DNB(ASA),∴DM=DN.
拓展应用:∵AC=4,△ABC为等腰直角三角形,∴AB=BC=![]() ,由归纳证明,可知△DMA≌△DNB(ASA),同理可得△BDM≌△DCN(ASA),∴S四边形DMBN=S△BDM+S△DBN=
,由归纳证明,可知△DMA≌△DNB(ASA),同理可得△BDM≌△DCN(ASA),∴S四边形DMBN=S△BDM+S△DBN=![]() =2.
=2.