题目内容
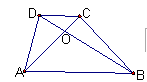
在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,CD=2,AB=5,则S△BOC:S△ADC=( )
A.2:5 B.5:2 C.2:7 D.5:7

A.2:5 B.5:2 C.2:7 D.5:7
D
∵AB∥CD,
∴△AOB∽△COD,
设△AOB的高为h1,△COD的高为h2,
则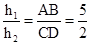 ,
,
∴S△BCD:S△ODC=(h1+h2):h2=7:2,
∴S△BCD:S△BOC=7:5,又∵S△BDC=S△ADC,
∴S△BOC:S△ADC=5:7.
故选D.
∴△AOB∽△COD,
设△AOB的高为h1,△COD的高为h2,
则
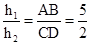 ,
,∴S△BCD:S△ODC=(h1+h2):h2=7:2,
∴S△BCD:S△BOC=7:5,又∵S△BDC=S△ADC,
∴S△BOC:S△ADC=5:7.
故选D.

练习册系列答案
相关题目
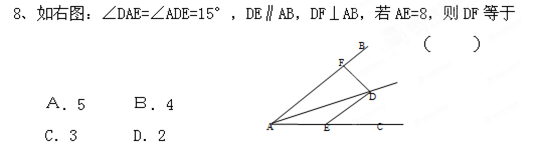
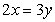 ,则
,则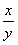 等于
等于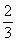
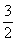
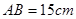 ,
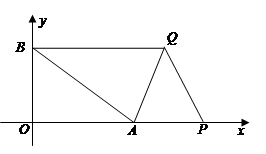
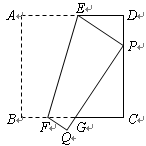
,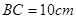 ,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动。如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与
,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动。如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与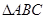 相似?
相似?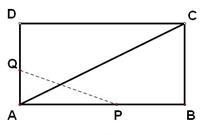
 与
与 是关于点O为位似中心的位似图形,他们的顶点都在格点上.
是关于点O为位似中心的位似图形,他们的顶点都在格点上.
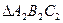 使它与的位似比等于3
使它与的位似比等于3