Question

【题目】画抛物线y=x2﹣2x﹣3的草图，并说出开口方向，对称轴，顶点坐标，增减性，最值．

Answer 1

【答案】见解析

【解析】试题分析：

（1）画二次函数图象，至少要描出5个点，其中顶点坐标必取，与坐标轴的交点，如果有，建议取，所取点，尽量在对称轴两边对称选取，否则图象不对称不完整.

（2）a大小决定开口方向，而a=1>0，故开口向上；对称轴为直线 ，顶点为即（1，-4）； 令x=0，则y=-3，得与y轴交点（0，-3）；令y=0,得方程x2﹣2x﹣3=0，解之得 ，得与x轴两个交点（3,0），（-1,0）.

（3）列表后描点，然后用平滑曲线连接各点，就得所求作的图象.

（4）根据草图，增减性，最值就一目了然.

解：列表，如下：

x	…	﹣1	0	1	2	3	…
y	…	0	﹣3	﹣4	﹣3	0	…

描点、连线，如图所示．

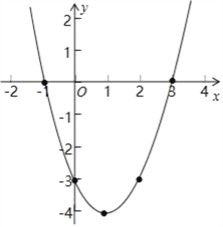
观察函数图象，可知：抛物线开口向上；对称轴为直线x=1；顶点坐标为（1，﹣4）；当x＜1时，y随x增大而减小，当x＞1时，y随x增大而增大；抛物线y=x2﹣2x﹣3存在最小值，最小值为﹣4．