Question

【题目】在平面直角坐标系中，O为原点，点A（﹣2，0），点B（0，2），点E，点F分别为OA，OB的中点．若正方形OEDF绕点O顺时针旋转，得正方形OE′D′F′，记旋转角为α．

（1）如图①，当α=90°时，求AE′，BF′的长；

（2）如图②，当α=135°时，求证AE′=BF′，且AE′⊥BF′；

（3）若直线AE′与直线BF′相交于点P，求点P的纵坐标的最大值（直接写出结果即可）．

Answer 1

【答案】（1）AE′=，BF′=；（2）答案见解析；（3）．

【解析】试题分析：（1）利用勾股定理即可求出的长．
（2）运用全等三角形的判定与性质、三角形的外角性质就可解决问题．
（3）首先找到使点P的纵坐标最大时点P的位置（点P与点D′重合时），然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值．

试题解析：(Ⅰ)当时,点E′与点F重合，如图①，

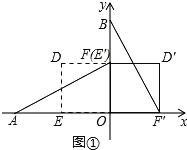
∵点A(2,0)点B(0,2)，

∴OA=OB=2.

∵点E，点F分别为OA，OB的中点，

∴OE=OF=1，

∵正方形OE′D′F′是正方形OEDF绕点O顺时针旋转得到的，

∴OE′=OE=1,OF′=OF=1.

在Rt△AE′O中，

在Rt△BOF′中，

∴AE′,BF′的长都等于

(Ⅱ)当时,如图②，

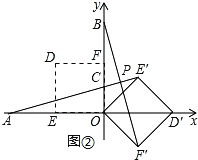
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转所得，

在△AOE′和△BOF′中，

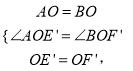
∴△AOE′≌△BOF′(SAS).

∴AE′=BF′,且∠OAE′=∠OBF′.

∵∠ACB=∠CAO+∠AOC=∠CBP+∠CPB，∠CAO=∠CBP，

∴AE′⊥BF′.

(Ⅲ) ，∴点P、B. A.O四点共圆，

∴当点P在劣弧OB上运动时，点P的纵坐标随着∠PAO的增大而增大，

∵OE′=1,∴点E′在以点O为圆心,1为半径的上运动,

∴当AP与相切时,∠E′AO(即∠PAO)最大，

此时点D′与点P重合，点P的纵坐标达到最大，

过点P作PH⊥x轴，垂足为H，如图③所示，

∴点P的纵坐标的最大值为