��Ŀ����
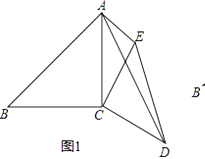
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,A��a,0����x����������һ��,C�ǵ�������һ��,CB��y��,��y�Ḻ������B��0,b��,��(a-3)2+|b+4|=0,S�ı���AOBC=16��
��1����C�����ꣻ
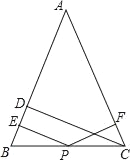
��2����ͼ2,��DΪ�߶�OB��һ����,��AD��ACʱ,��ODA�Ľ�ƽ�������CAE�Ľ�ƽ���ߵķ����ӳ��߽��ڵ�P,���APD�Ķ�����
��3����ͼ3,��D�����߶�OB���˶�ʱ,��DM��AD��BC��M��,��BMD����DAO��ƽ���߽���N��,��D�����˶�������,��N�Ĵ�С�Ƿ�仯��������,�����ֵ,���仯,˵�����ɣ�

���𰸡�(1) C��5����4��;(2)90��;(3)������.
����������1�����÷Ǹ����ĺ�Ϊ�㣬����ֱ�Ϊ�㣬���a��b���ɣ�
��2����ͬ�ǵ������Ⱥͽ�ƽ���ߵ����弴�ɣ�
��3�����ý�ƽ���ߵ�����ͻ������ǵĹ�ϵ����֤�����ɣ�
��1������a��3��2+|b+4|=0��
��a��3=0��b+4=0��
��a=3��b=��4��
��A��3��0����B��0����4����
��OA=3��OB=4��
��S�ı���AOBC=16��
��0.5��OA+BC����OB=16��
��0.5��3+BC����4=16��
��BC=5��
��C�ǵ�������һ�㣬CB��y�ᣬ
��C��5����4����
��2����ͼ��
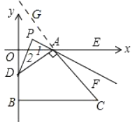
�ӳ�CA����AF�ǡ�CAE�Ľ�ƽ���ߣ�
���CAF=0.5��CAE��
�ߡ�CAE=��OAG��
���CAF=0.5��OAG��
��AD��AC��
���DAO+��OAG=��PAD+��PAG=90�㣬
�ߡ�AOD=90�㣬
���DAO+��ADO=90�㣬
���ADO=��OAG��
���CAF=0.5��ADO��
��DP�ǡ�ODA�Ľ�ƽ������
���ADO=2��ADP��
���CAF=��ADP��
�ߡ�CAF=��PAG��
���PAG=��ADP��
���APD=180�㩁����ADP+��PAD��=180�㩁����PAG+��PAD��=180�㩁90��=90��
������APD=90��
��3�����䣬��ANM=45�����ɣ���ͼ��
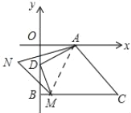
�ߡ�AOD=90�㣬
���ADO+��DAO=90�㣬
��DM��AD��
���ADO+��BDM=90�㣬
���DAO=��BDM��
��NA�ǡ�OAD��ƽ���ߣ�
���DAN=0.5��DAO=0.5��BDM��
��CB��y�ᣬ
���BDM+��BMD=90�㣬
���DAN=0.5��90�㩁��BMD����
��MN�ǡ�BMD�Ľ�ƽ���ߣ�
���DMN=0.5��BMD��
���DAN+��DMN=0.5��90�㩁��BMD��+0.5��BMD=45��
����DAM�У���ADM=90�㣬
���DAM+��DMA=90�㣬
����AMN��
��ANM=180�㩁����NAM+��NMA��=180�㩁����DAN+��DAM+��DMN+��DMA��=180�㩁[����DAN+DMN��+����DAM+��DMA��] =180�㩁��45��+90�㣩=45�㣬
��D�����˶������У���N�Ĵ�С���䣬�����ֵΪ45��

 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�