题目内容
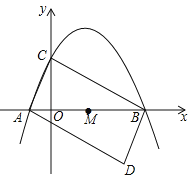
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG//DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,求证四边形AGBD是矩形.

【答案】(1)见详解;(2)见详解.
【解析】
(1)证三角形全等根据边角边即可证明;
(2)先证明ADBG是平行四边形再证明有一个角是直角的平行四边形是矩形即可证明;
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠BAD=∠C,AD//BC,
又∵E、F分别为边AB、CD的中点,
∴AE=![]() AB,CF=
AB,CF=![]() CD,
CD,
∴AE=CF,
∴△ADE≌△CBF(SAS);
(2)∵AD//BC,AG//DB,
∴四边形AGBD是平行四边形,
∵四边形BEDF是菱形,
∴BE=DE,
∵E、F分别为边AB、CD的中点,
∴AE=BE,
∴BE=DE=AE,
∴∠ADE=∠EAD,∠EDB=∠EBD,
∵∠EAD+∠EDA+∠EDB+∠EBD=180°,
∴∠EDA+∠EDB=90°,
∴∠ADB=90°,
∴四边形ADBG是矩形,

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案【题目】我校开展的社团活动有:A.动漫社团;B.轮滑社团:C.音乐社团;D.诗歌社团;E.书法社团.学生管理中心为了了解全校500名学生的社团需求,开展了一次调查研究,请将下面的调查过程补全
抽样调查:从七、八、九三个年级中随机抽取男女生各20名进行问卷调研;
收集数据:抽样方法确定后,学生管理中心收集到如下数据(社团项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B
A,C,E,D,B,A,B,E,C,A
D,D,B,B,C,C,A,A,E,B
C,B,D,C,A,C,C,A,C,E
整理、描述数据:划记、整理、描述样本数据、绘制统计图如下,请补全统计表和统计图
社团项目 | 划记 | 人数 |
A动漫社 |
| 8 |
B轮滑社 | ||
C音乐社 |
| 12 |
D诗歌社 | ||
E书法社 |
| 6 |
合计 | 40 | 40 |
分析数据、推断结论

(1)在扇形统计图中,“B轮滑社团”所在的扇形的圆心角等于 度;
(2)根据学生管理中心获得的样本数据,估计全校大约有 名同学选择D社团.