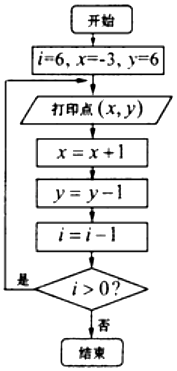
��Ŀ����
����Ŀ���ڡ������ۡ�ģʽ�ı����£�ij�������۹�˾Ϊ�ƹ����·ֵ꣬�ƻ���S�е�A������ֵ꣮Ϊ��ȷ���ڸ�������ֵ�ĸ������ù�˾�Ը����ѿ���ֵ�����������������˳���������õ����б���x��ʾ�ڸ�������ֵ�ĸ�����y��ʾ��x���ֵ��������֮�ͣ�
x������ | 2 | 3 | 4 | 5 | 6 |
y������Ԫ�� | 2.5 | 3 | 4 | 4.5 | 6 |
���ù�˾�Ѿ��������жϣ��������Իع�ģ�����y��x�Ĺ�ϵ����y����x�����Իع鷽��y= ![]() ��
��
������ù�˾��A����õ���������z����λ������Ԫ����x��y֮��Ĺ�ϵΪz=y��0.05x2��1.4�����ϣ����е����Իع鷽�̣�����ù�˾Ӧ��A��������ٸ��ֵ�ʱ������ʹA��ƽ��ÿ���ֵ�����������
�ο���ʽ�� ![]() =
= ![]() x+a��
x+a�� ![]() =
=  =
=  ��a=
��a= ![]() ��
�� ![]() ��
��
���𰸡��⣺���� ![]() =4��
=4�� ![]() =4��
=4�� ![]() =
= 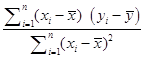 =
= ![]() =0.85��a=
=0.85��a= ![]() ��
�� ![]() =4��4��0.85=0.6�� ��y����x�����Իع鷽��y=0.85x+0.6��
=4��4��0.85=0.6�� ��y����x�����Իع鷽��y=0.85x+0.6��
����z=y��0.05x2��1.4=��0.05x2+0.85x��0.8��
A��ƽ��ÿ���ֵ��������t= ![]() =��0.05x��
=��0.05x�� ![]() +0.85=��0.01��5x+
+0.85=��0.01��5x+ ![]() ��+0.85��
��+0.85��
��x=4ʱ��tȡ�����ֵ��
�ʸù�˾Ӧ��A������4���ֵ�ʱ������ʹA��ƽ��ÿ���ֵ�����������
����������������ع�ϵ�����ɵ�y����x�����Իع鷽�̣� �������A��ƽ��ÿ���ֵ�����������û�������ʽ���ɵý��ۣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij����Ϊ�˽����۽γ�̨������������֮��Ĺ�ϵ���õ����ͳ�����ݱ����������ݱ��ɵûع�ֱ�߷��� ![]() ������
������ ![]() ��
�� ![]() ���ݴ�ģ��Ԥ�������Ϊ9��Ԫʱ�����۽γ�̨��Ϊ�� ��
���ݴ�ģ��Ԥ�������Ϊ9��Ԫʱ�����۽γ�̨��Ϊ�� ��
������x����Ԫ�� | 2 | 3 | 4 | 5 | 6 |
���۽γ�y��̨���� | 3 | 4 | 6 | 10 | 12 |
A.17
B.18
C.19
D.20