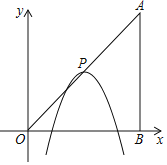题目内容
【题目】已知抛物线y=ax2经过点A(2,1).

(1) 求a的值;
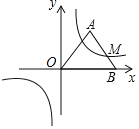
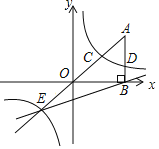
(2) 如图1,点M为x轴负半轴上一点,线段AM交抛物线于N.若△OMN为等腰三角形,求点N的坐标;
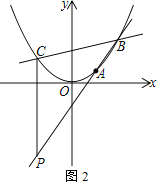
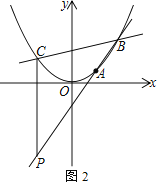
(3) 如图2,直线y=kx-2k+3交抛物线于B、C两点,过点C作CP⊥x轴,交直线AB于点P,请说明点P一定在某条确定的直线上运动,求出这条直线的解析式.
【答案】(1)![]() ;(2)N(﹣1,
;(2)N(﹣1,![]() );(3)y=x﹣3.
);(3)y=x﹣3.
【解析】
(1)A(2,1)代入抛物线方程,解方程即可得到a的值;
(2)设点M(m,0),求出AM所在直线的表达式,MN=ON时,过点N作NH⊥OM,求出OH,HN的长,得出N的坐标,把N点坐标代入抛物线表达式求解即可得出结论;
(3)设:点C(x1,y1),B(x2,y2),P(x1,y),则:![]() x2=kx﹣2k+3,由根与系数的关系得:x1+x2=4k,x1x2=8k﹣12,…①,y2
x2=kx﹣2k+3,由根与系数的关系得:x1+x2=4k,x1x2=8k﹣12,…①,y2![]() ②,把A、B坐标代入直线方程,解得AB所在的直线方程,把点P(x1,y)、①、②代入方程,整理即可得到结论.
②,把A、B坐标代入直线方程,解得AB所在的直线方程,把点P(x1,y)、①、②代入方程,整理即可得到结论.
(1)A(2,1)代入抛物线方程,解得:a![]() ;
;
(2)设点M(m,0),把点A、M坐标代入直线表达式得:
AM所在直线的表达式为:y![]() x
x![]() .
.
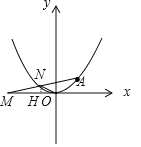
从图象位置关系看,△OMN为等腰三角形时,只有MN=ON这一种情况,过点N作NH⊥OM,则OH=MH![]() ,HN=MHtan∠AMH
,HN=MHtan∠AMH![]() ,则N(
,则N(![]() ,
,![]() ),把N点坐标代入抛物线表达式解得:m=﹣2,m=4(舍去);则N(-1,
),把N点坐标代入抛物线表达式解得:m=﹣2,m=4(舍去);则N(-1,![]() ).
).
经验证:MN=OM,OM=ON无解.故:N(﹣1,![]() );
);
(3)设:点C(x1,y1),B(x2,y2),P(x1,y),则:![]() x2=kx﹣2k+3,则:
x2=kx﹣2k+3,则:![]() ②,把A、B坐标代入直线方程,解得:
②,把A、B坐标代入直线方程,解得:
AB所在的直线方程为:y![]() ,把点P(x1,y)、①、②代入上式,整理得:y=x1﹣3,这条直线的解析式为:y=x﹣3.
,把点P(x1,y)、①、②代入上式,整理得:y=x1﹣3,这条直线的解析式为:y=x﹣3.