Question

【题目】如图，在△ABC中，D是AB的中点，E是CD的中点， 过点C作CF//AB交AE的延长线于点F，连接BF．

(1) 求证：DB＝CF；

(2) 如果AC＝BC，试判断四边形BDCF的形状，并证明你的结论．

Answer 1

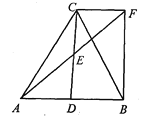
【答案】(1)证明见解析；（2）四边形BDCF是矩形，理由见解析.

【解析】试题分析：（1）根据CF∥AB，可知∠DAE=∠CFE，得出△ADE≌△FCE，再根据等量代换可知DB=CF，

（2）根据DB=CF，DB∥CF，可知四边形BDCF为平行四边形，再根据AC=BC，AD=DB，得出四边形BDCF是矩形．

试题解析：（1）证明：∵CF∥AB，

∴∠DAE=∠CFE，

在△ADE和△FCE中，

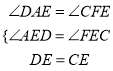
∴△ADE≌△FCE（AAS），

∴AD=CF，

∵AD=DB，

∴DB=CF；

（2）四边形BDCF是矩形，

证明：∵DB=CF，DB∥CF，

∴四边形BDCF为平行四边形，

∵AC=BC，AD=DB，

∴CD⊥AB，

∴平行四边形BDCF是矩形．