题目内容
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
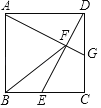
(1)证明:△ADG≌△DCE;(2)连接BF,证明:AB=FB.
【答案】(1)见解析;(2)见解析.
【解析】
(1)依据正方形的性质以及垂线的定义,即可得到∠ADG=∠C=90°,AD=DC,∠DAG=∠CDE,即可得出△ADG≌△DCE;
(2)延长DE交AB的延长线于H,根据△DCE≌△HBE,即可得出B是AH的中点,进而得到AB=FB.
解:(1)∵四边形ABCD是正方形,
∴∠ADG=∠C=90°,AD=DC,
又∵AG⊥DE,
∴∠DAG+∠ADF=90°=∠CDE+∠ADF,
∴∠DAG=∠CDE,
∴△ADG≌△DCE(ASA);
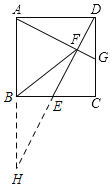
(2)如图所示,延长DE交AB的延长线于H,
∵E是BC的中点,
∴BE=CE,
又∵∠C=∠HBE=90°,∠DEC=∠HEB,
∴△DCE≌△HBE(ASA),
∴BH=DC=AB,
即B是AH的中点,
又∵∠AFH=90°,
∴Rt△AFH中,BF=![]() AH=AB.
AH=AB.

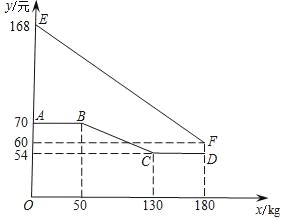
【题目】某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量![]() 件
件![]() 与时间
与时间![]() 天
天![]() 的关系如下表:
的关系如下表:
时间 | 1 | 3 | 5 | 10 | 36 |
|
日销售量 | 94 | 90 | 86 | 76 | 24 |
|
已知未来40天内,前20天该商品每天的价格![]() 元
元![]() 件
件![]() 与时间t的函数关系式为
与时间t的函数关系式为![]() (
(![]() ,且t为整数),后20天该商品每天的价格
,且t为整数),后20天该商品每天的价格![]() 元
元![]() 件
件![]() 与时间t的函数关系式为
与时间t的函数关系式为![]() (
(![]() ,且t为整数).
,且t为整数).
![]() 求m与t之间的函数关系式;
求m与t之间的函数关系式;
![]() 未来40天内,后20天中哪一天的日销售利润最大
未来40天内,后20天中哪一天的日销售利润最大![]() 最大日销售利润是多少.
最大日销售利润是多少.
![]() 在实际销售的前20天中,该公司决定每销售一件商品,就捐赠
在实际销售的前20天中,该公司决定每销售一件商品,就捐赠![]() 元给希望工程
元给希望工程![]() 公司查阅销售记录发现,前20天中,扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
公司查阅销售记录发现,前20天中,扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.