题目内容
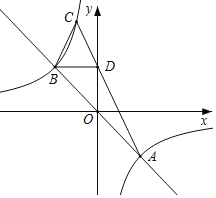
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.
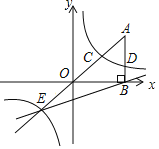
【答案】(1)反比例函数的解析式为y=![]() ;(2)直线BE的解式为:y=
;(2)直线BE的解式为:y=![]() x﹣2;(3)S△OEB=12.
x﹣2;(3)S△OEB=12.
【解析】(1)利用待定系数法求反比例函数的解析式;
(2)根据点A的坐标可求得直线OA的解析式,联立直线OA和反比例函数解析式列方程组可得点E的坐标,再利用待定系数法求BE的解析式;
(3)根据三角形的面积公式计算即可.
(1)∵A点的坐标为(a,6),AB⊥x轴,
∴AB=6,
∵cos∠OAB═![]() ,
,
∴![]() ,
,
∴OA=10,
由勾股定理得:OB=8,
∴A(8,6),
∴D(8,![]() ),
),
∵点D在反比例函数的图象上,
∴k=8×![]() =12,
=12,
∴反比例函数的解析式为:y=![]() ;
;
(2)设直线OA的解析式为:y=bx,
∵A(8,6),
∴8b=6,b=![]() ,
,
∴直线OA的解析式为:y=![]() x,
x,
则![]() ,x=±4,
,x=±4,
∴E(-4,-3),
设直线BE的解式为:y=mx+n,
把B(8,0),E(-4,-3)代入得:![]() ,
,
解得: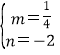 ,
,
∴直线BE的解式为:y=![]() x-2;
x-2;
(3)S△OEB=![]() OB|yE|=
OB|yE|=![]() ×8×3=12.
×8×3=12.

【题目】“十一”黄金周期间,各地景区游人如织,其中淮安动物园在9月30日的游客人数为1万人,接下来的七天假期中每天接待的游客人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 (单位:万人) |
|
|
|
|
|
|
|
(1)请根据计算判断七天内游客人数最多的是哪天,有多少万人?
(2)若以9月30日的游客人数1万人为标准,每人门票均为10元,问黄金周期间淮安动物园平均每天门票多收入多少万元?