题目内容
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(6,6),(6,0),抛物线y=﹣(x﹣m)2+n的顶点P在折线OA﹣AB上运动.
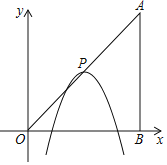
(1)当点P在线段OA上运动时,抛物线y=﹣(x﹣m)2+n与y轴交点坐标为(0,c).
①用含m的代数式表示n,
②求c的取值范围.
(2)当抛物线y=﹣(x﹣m)2+n经过点B时,求抛物线所对应的函数表达式;
(3)当抛物线与△ABO的边有三个公共点时,直接写出点P的坐标.
【答案】(1)①n=m;②c的取值范围为﹣30≤c≤![]() ;(2)y=﹣(x﹣6)2;(3)满足条件的点P坐标为(1,1)或(6,6)或(6,
;(2)y=﹣(x﹣6)2;(3)满足条件的点P坐标为(1,1)或(6,6)或(6,![]() )
)
【解析】
(1)①设直线OA的解析式为y=kx,把点(6,6)代入可得k=1,推出y=x.因为y=-(x-m)2+n的顶点P在OA上,推出n=m.②由题意:y=-x2+2mx-m2+m,由抛物线与y轴交点坐标为(0,c),推出c=-m2+m,根据0≤m≤6,利用二次函数的性质即可解决问题.
(2)把B(6,0)代入抛物线的解析式即可解决问题.
(3)分三种情形①当抛物线经过点O时,抛物线与△ABO的边有三个公共点,
②当抛物线经过点A时,抛物线与△ABO的边有三个公共点,此时P(6,6).
③当点P在AB上运动,抛物线与OA只有一个公共点时,抛物线与△ABO的边有三个公共点.
解:(1)①设直线OA的解析式为y=kx,∵经过(6,6),
∴6k=6,
∴k=1,
∴y=x.
∵y=﹣(x﹣m)2+n的顶点P在OA上,
∴n=m.
②由题意:y=﹣x2+2mx﹣m2+m,
∵抛物线与y轴交点坐标为(0,c),
∴c=﹣m2+m,
∵点P在线段OA上,
∴0≤m≤6,﹣![]() =﹣
=﹣![]() =
=![]() ,
,
∵0<![]() <6,
<6,
∴当m=![]() 时,c=﹣(
时,c=﹣(![]() )2+
)2+![]() =
=![]() ,
,
当m=6时,c=﹣62+6=﹣30,
∴c的取值范围为﹣30≤c≤![]() .
.
(2)当点P在线段OA上时,
∵抛物线经过B(6,0),
∴﹣(6﹣m)2+m=0,
∴m=4或9(舍弃),
∴y=﹣(x﹣4)2+4,
当点P在线段AB上时,点P与点B重合,
∴m=6,
∴y=﹣(x﹣6)2.
(3)①当抛物线经过点O时,抛物线与△ABO的边有三个公共点,
把(0,0)代入抛物线y=﹣(x﹣m)2+m得到m=1或0(舍弃),此时P(1,1).
②当抛物线经过点A时,抛物线与△ABO的边有三个公共点,此时P(6,6).
③当点P在AB上运动,抛物线与OA只有一个公共点时,抛物线与△ABO的边有三个公共点,
由![]() 消去y得到x2﹣11x+36﹣n=0,
消去y得到x2﹣11x+36﹣n=0,
由题意△=0,∴121﹣4(36﹣n)=0,
∴n=![]() ,
,
∴P(6,![]() ),
),
综上所述,满足条件的点P坐标为(1,1)或(6,6)或(6,![]() )
)
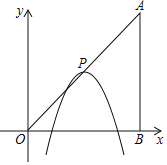

 阅读快车系列答案
阅读快车系列答案