题目内容
、(本题12分)如图,设抛物线C1: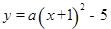 , C2:
, C2: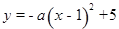 ,C1与C2的交点为A, B,点A的坐标是
,C1与C2的交点为A, B,点A的坐标是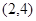 ,点B的横坐标是-2.
,点B的横坐标是-2.
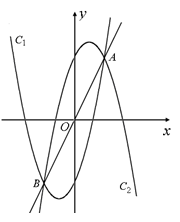
小题1:(1)求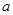 的值及点B的坐标;
的值及点B的坐标;
小题2:(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG.记过C2顶点M的直线为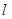 ,且
,且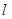 与x轴交于点N.
与x轴交于点N.
① 若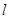 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
② 若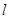 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.
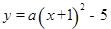 , C2:
, C2: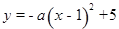 ,C1与C2的交点为A, B,点A的坐标是
,C1与C2的交点为A, B,点A的坐标是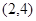 ,点B的横坐标是-2.
,点B的横坐标是-2.
小题1:(1)求
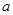 的值及点B的坐标;
的值及点B的坐标; 小题2:(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG.记过C2顶点M的直线为
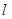 ,且
,且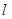 与x轴交于点N.
与x轴交于点N.① 若
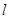 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;② 若
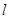 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.小题1:解:(1)∵ 点A
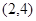 在抛物线C1上,∴ 把点A坐标代入
在抛物线C1上,∴ 把点A坐标代入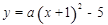 得
得 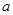 =1.
=1. ∴ 抛物线C1的解析式为
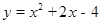 ,
,设B(-2,b), ∴ b=-4, ∴ B(-2,-4) .
小题2:
(2)①如图1,
∵ M(1, 5),D(1, 2), 且DH⊥x轴,∴ 点M在DH上,MH="5."
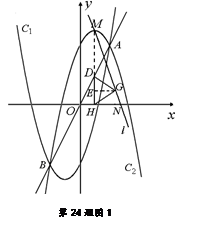 过点G作GE⊥DH,垂足为E,
过点G作GE⊥DH,垂足为E,由△DHG是正三角形,可得EG=
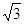 , EH=1,
, EH=1,∴ ME=4. 设N ( x, 0 ), 则 NH=x-1,
由△MEG∽△MHN,得
 ,
,∴
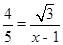 , ∴
, ∴ 
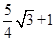 ,
,∴ 点N的横坐标为
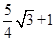 .
. ② 当点D移到与点A重合时,如图2,
直线
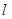 与DG交于点G,此时点N的横坐标最大.
与DG交于点G,此时点N的横坐标最大.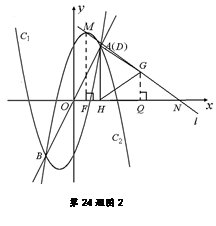 过点G,M作x轴的垂线,垂足分别为点Q,F, 设N(x,0),
过点G,M作x轴的垂线,垂足分别为点Q,F, 设N(x,0),∵ A (2, 4), ∴ G (
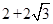 , 2),
, 2),∴ NQ=
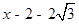 ,NF =
,NF =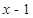 , GQ="2," MF =5.
, GQ="2," MF =5.∵ △NGQ∽△NMF,
∴
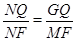 ,
,∴
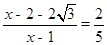 ,
,∴
 .
. 当点D移到与点B重合时,如图3,直线
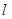 与DG交于点D,即点B,
与DG交于点D,即点B, 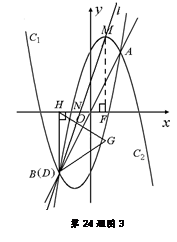 此时点N的横坐标最小.
此时点N的横坐标最小.∵ B(-2, -4), ∴ H(-2, 0), D(-2, -4),
设N(x,0),
∵ △BHN∽△MFN, ∴
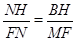 ,
,∴
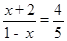 , ∴
, ∴ 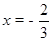 . ∴ 点N横坐标的范围为
. ∴ 点N横坐标的范围为 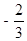 ≤x≤
≤x≤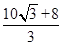 且x≠0.
且x≠0. 略

练习册系列答案
相关题目
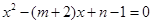 的两根:
的两根:
 交x轴于点D,试求直线
交x轴于点D,试求直线 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由

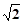 MD;
MD;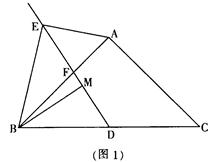
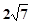 ,求tan∠ACP的值.
,求tan∠ACP的值.
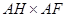 的值。
的值。
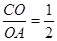 ,S△COD=12,则△ABC的面积是 .
,S△COD=12,则△ABC的面积是 .