题目内容
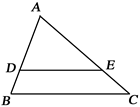
如图,在△ABC中,DE∥BC,AD =2DB,△ABC的面积为36,则△ADE的面积为

| A.81 | B.54 |
| C.24 | D.16 |
D
分析:由于DE∥BC,根据平行线分线段成比例定理的推论可得△ADE∽△ABC,又AD=2BD,易得AD:AB=2:3,再根据相似三角形的面积比等于相似比的平方可得S△ADE:S△ABC=4:9,结合S△ABC=36,进而可求△ADE的面积.
解答:解:
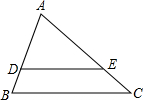
∵DE∥BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=(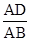 )2,
)2,
又∵AD=2BD,
∴AD:AB=2:3,
∴S△ADE:S△ABC=(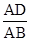 )2=4:9,
)2=4:9,
∵S△ABC=36,
∴S△ADE=16.
故选D.
解答:解:

∵DE∥BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=(
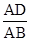 )2,
)2,又∵AD=2BD,
∴AD:AB=2:3,
∴S△ADE:S△ABC=(
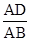 )2=4:9,
)2=4:9,∵S△ABC=36,
∴S△ADE=16.
故选D.

练习册系列答案
相关题目
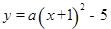 , C2:
, C2: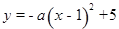 ,C1与C2的交点为A, B,点A的坐标是
,C1与C2的交点为A, B,点A的坐标是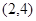 ,点B的横坐标是-2.
,点B的横坐标是-2.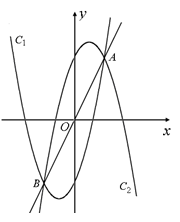
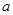 的值及点B的坐标;
的值及点B的坐标; 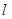 ,且
,且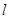 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;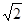
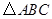 中,
中,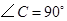 ,在
,在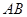 边上取一点
边上取一点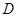 ,使
,使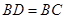 ,过
,过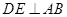 交
交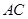 于
于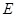 ,
,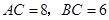 .求
.求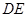 的长.
的长.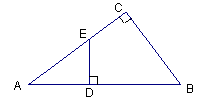
 对折,折痕为
对折,折痕为 ,矩形
,矩形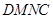 与矩形
与矩形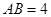 .则
.则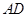 的长 .矩形
的长 .矩形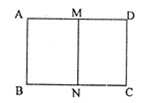
 B
B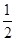 ,则点A
,则点A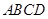 边长为4,
边长为4,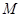 、
、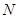 分别是
分别是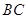 、
、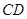 上的两个动点,当
上的两个动点,当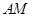 和
和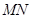 垂直,
垂直,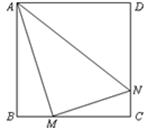
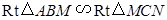 ;
;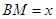 ,梯形
,梯形 的面积为
的面积为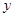 ,求
,求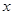 之间的函数关系式;
之间的函数关系式;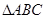 中,
中,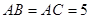 ,
,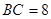 ,
,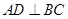 ,垂足为
,垂足为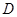 ,
,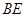 是边
是边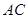 上的中线,
上的中线, 与
与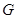 ,那么
,那么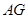 的长为…………………………………( )
的长为…………………………………( )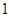 ;
;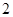 ;
;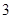 ;
;