题目内容
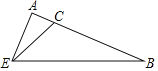
【题目】如图,Rt△ABE中,∠A=90°,点C在AB上,∠CEB=2∠AEC=45°.
(1)求∠B的度数;
(2)求证:BC=2AE.
【答案】(1)∠B=22.5°;(2)证明见解析.
【解析】
(1)根据∠CEB=2∠AEC=45°可求得∠AEB=67.5°,根据直角三角形两锐角互余,即可求出∠B的度数;
(2)取BC的中点D,作DF⊥AB交BE于F,连接CF,根据垂直平分线的性质定理可得CF=BF,BC=2BD,可证△CEF是等腰直角三角形,根据等腰直角三角形的性质CE=CF=BF,证明△ACE≌△DFB根据全等三角形的性质定理即可得出结论.
(1)解:∵∠CEB=2∠AEC=45°.
∴∠AEC=22.5°,
∴∠AEB=45°+22.5°=67.5°,
∵∠A=90°,
∴∠B=90°﹣∠AEB=22.5°;
(2)证明:取BC的中点D,作DF⊥AB交BE于F,连接CF,如图所示:

则BC=2BD,BF=CF,
∴∠BCF=∠B=22.5°,
∵∠BCE=∠A+∠AEC=112.5°,
∴∠ECF=112.5°﹣22.5°=90°,
∵∠CEB=45°,
∴△CEF是等腰直角三角形,
∴CE=CF=BF,
在△ACE和△DFB中,
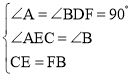 ,
,
∴△ACE≌△DFB(AAS),
∴AE=BD,
∴BC=2AE.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目