题目内容
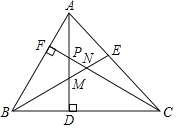
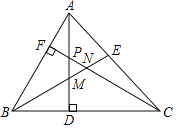
【题目】如图,在△ABC中,∠ABC=60°,∠BAC=75°,AD,CF分别是BC、AB边上的高且相交于点P,∠ABC的平分线BE分别交AD、CF于M、N.以下四个结论:①△PMN等边三角形;②除了△PMN外,还有4个等腰三角形;③△ABD≌△CPD;④当DM=2时,则DC=6.其中正确的结论是:_____(填序号).
【答案】①②③④.
【解析】
由已知条件,根据三角形内角和等于180°、角的平分线的性质求得各个角的度数,然后利用等腰三角形的判定进行找寻,注意做到由易到难.
∵∠ABC=60°,∠BAC=75°,AD,CF分别是BC,AB边上的高,
∴∠DAC=45°,又∵∠ACB=45°,
∴△ADC为等腰直角三角形.
∵∠ABC的平分线BE分别交AD,CF于M,N
∴∠ABM=30°,
又∵∠BAM=30°
∴△AMB为等腰三角形.
由题意可知∵∠NBC=∠NCB=30°
∴△BNC为等腰三角形.
∠PMN=∠MNP=60°
∴△MNP为等边三角形,故①正确;
∵∠ABE=30°,∠BAC=75°,
∴∠BEA=75°,
∴△ABE为等腰三角形;
∴除了△PMN外,还有4个等腰三角形,故②正确;
∵AD,CF分别是BC,AB边上的高,
∴∠ADB=∠BFC=90°,
∴∠BAD=∠ABD=∠ABD+∠BCF=90°,
∴∠BAD=∠DCP,
∵∠ADB=∠PDC=90°,AD=CD,
∴△ABD≌△CPD(ASA),故③正确;
在直角三角形BDM中,
∵MD=2,∠MBD=30°,
∴BM=4,
在等腰三角形AMB中,BM=AM,
∴AD=AM+MD=6,
在等腰直角三角形ADC中,AD=DC,
∴DC=6,故④正确;
故答案为:①②③④.

【题目】为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
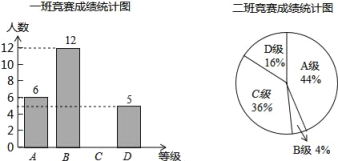
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
一班 | a | b | 90 | 106.24 |
二班 | 87.6 | 80 | c | 138.24 |
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.