题目内容
已知：如图，∠ACB=90°，AC=BC , AD = BE, ∠CAD=∠CBE ,
小题1:（1）判断△DCE的形状，并说明你的理由；
小题2:（2）当BD:CD=1:2时，∠BDC=135°时，求sin∠BED的值.
小题1:（1）判断△DCE的形状，并说明你的理由；
小题2:（2）当BD:CD=1:2时，∠BDC=135°时，求sin∠BED的值.
小题1:(1)∵ AC=BC , AD = BE, ∠CAD=∠CBE ,
∴ △ADC≌△BEC……………………………………..1分
∴ DC=EC,∠1=∠2. ……………………………………2分
∵ ∠1+∠BCD=90°，
∴ ∠2+∠BCD=90°.
所以 △DCE是等腰直角三角形
小题2:(2) ∵ △DCE是等腰直角三角形.
∴ ∠CDE=45°.
∵ ∠BDC=135°，
∴ ∠BDE=90°……………………………………………………………………………….4分
∵ BD:CD=1:2,
设BD=x，则CD=2x，DE=
，BE=3x.∴
…略
练习册系列答案
阅读快车系列答案
相关题目
的位置如图所示，则
的值为
）
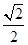
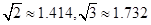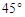．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面的倾斜角为
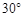，若新坡角下需留3米的人行道，问离原坡角10米的建筑物是否需要拆除？
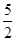
的坡面向上走50米，则此人离地面的高度为( )
