题目内容
如图,反比例函数y=
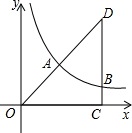
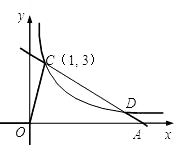
图象在第一象限的分支上有一点C(1,3),过点C的直线y=k2x+b(k2<0,b为常数)与x轴交于点A(a,0).
(1)求反比例函数的解析式;
(2)求A点横坐标a和k2之间的函数关系式;
(3)当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时,求△COA的面积.
| k1 |
| x |
(1)求反比例函数的解析式;
(2)求A点横坐标a和k2之间的函数关系式;
(3)当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时,求△COA的面积.

(1)∵点C(1,3)在反比例函数图象上
∴K1=1×3=3,
∴y=
;
(2)由题意得
,消去b,得a=1-
;
(3)当X=3时,Y=
=1,
∴D(3,1)
∵C(1,3)、D(3,1)在直线y=k2x+b上,
∴
∴
∴y=-x+4,令y=0,则x=4
∴A(4,0)
∴S△COA=
×4×3=6.
∴K1=1×3=3,
∴y=
| 3 |
| x |
(2)由题意得
|
| 3 |
| K2 |
(3)当X=3时,Y=
| 3 |
| 3 |
∴D(3,1)
∵C(1,3)、D(3,1)在直线y=k2x+b上,
∴
|
|
∴y=-x+4,令y=0,则x=4
∴A(4,0)
∴S△COA=
| 1 |
| 2 |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
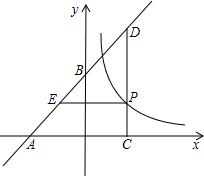
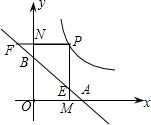 ⊥x轴,PN⊥y轴,垂足分别为M,N.PM与直线AB交于点E,PN的延长线与直线AB交于点F.
⊥x轴,PN⊥y轴,垂足分别为M,N.PM与直线AB交于点E,PN的延长线与直线AB交于点F.