题目内容
【题目】如图,点P( ![]() +1,
+1, ![]() ﹣1)在双曲线y=
﹣1)在双曲线y= ![]() (x>0)上.
(x>0)上.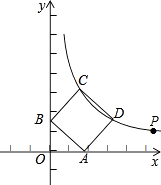
(1)求k的值;
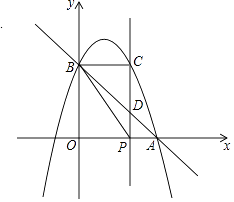
(2)若正方形ABCD的顶点C,D在双曲线y= ![]() (x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
【答案】
(1)解:点P( ![]() ,
, ![]() )在双曲线
)在双曲线 ![]() 上,
上,
将x= ![]() ,y=
,y= ![]() 代入解析式可得:
代入解析式可得:
k=2;
(2)解:过点D作DE⊥OA于点E,过点C作CF⊥OB于点F, 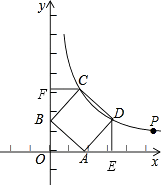
∵四边形ABCD是正方形,
∴AB=AD=BC,∠CBA=90°,
∴∠FBC+∠OBA=90°,
∵∠CFB=∠BOA=90°,
∴∠FCB+∠FBC=90°,
∴∠FBC=∠OAB,
在△CFB和△AOB中,
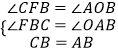 ,
,
∴△CFB≌△AOB(AAS),
同理可得:△BOA≌△AED≌△CFB,
∴CF=OB=AE=b,BF=OA=DE=a,
设A(a,0),B(0,b),
则D(a+b,a)C(b,a+b),
可得:b(a+b)=2,a(a+b)=2,
解得:a=b=1.
所以点C的坐标为:(1,2).
【解析】(1)由待定系数法把P坐标代入解析式即可;(2)C、D均在双曲线上,它们的坐标就适合解析式,设出C坐标,再由正方形的性质可得△CFB≌△AOB△BOA≌△AED≌△CFB,代入解析式得b(a+b)=2,a(a+b)=2,即可求出C坐标.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个,付款总额不得超过11815元.已知:厂家两种球的批发价如(表![]() )、商场在某两天的零售信息如(表
)、商场在某两天的零售信息如(表![]() ):
):
品名 | 厂家批发价(元/个) |
篮球 | 130 |
排球 | 100 |
(表![]() )
)
篮球(个) | 排球(个) | 零售总价(元) | |
第一天 | 8 | 5 | 1880 |
第二天 | 6 | 10 | 2160 |
(表![]() )
)
请解决以下问题:
(1)求出体育商场出售篮球和排球的零售单价.
(2)该采购员最多可从厂家购进篮球多少个.
(3)若该商场把这100个球全部以零售价售出,为使商场的利润不低于2580元,则采购员采购的方案有哪几种?该商场最多可盈利__________元.