题目内容
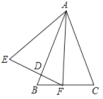
【题目】如图，在菱形ABCD中，tan∠ABC= 
，P为AB上一点，以PB为边向外作菱形PMNB，连结DM，取DM中点E，连结AE，PE，则 
的值为（ ）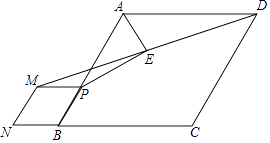
A.
B.
C.
D.
【答案】C
【解析】解：如图，延长AE交MP的延长线于F，作AH⊥PF于H．
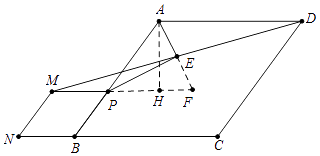
∵AD∥CN∥PM，
∴∠ADE=∠EMF，
∵ED=EM，∠AED=∠MEF，
∴△AED≌△FEM，
∴AE=EF．AD=MF=AB，
∵PM=PB，
∴PA=PF，
∴PE⊥AF，∠APE=∠FPE，
∵∠APF=∠ABC，
∴tan∠APF=tan∠ABC= 
= 
，设AH=4k，PH=3k，则PA=PF=5k，FH=2k，AF= 
=2 
k，
∵ 
PFAH= AFPE，
∴PE=2 k，AE= k
∴AE：PE= k：2 =1：2，
所以答案是：C．
【考点精析】利用等腰三角形的性质和勾股定理的概念对题目进行判断即可得到答案，需要熟知等腰三角形的两个底角相等（简称：等边对等角）；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
练习册系列答案
考前必练系列答案
相关题目
【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个，付款总额不得超过11815元．已知：厂家两种球的批发价如(表
)、商场在某两天的零售信息如(表
)：
品名 | 厂家批发价(元/个) |
篮球 | 130 |
排球 | 100 |
(表)
篮球(个) | 排球(个) | 零售总价(元) | |
第一天 | 8 | 5 | 1880 |
第二天 | 6 | 10 | 2160 |
(表)
请解决以下问题：
（1）求出体育商场出售篮球和排球的零售单价．
（2）该采购员最多可从厂家购进篮球多少个．
（3）若该商场把这100个球全部以零售价售出，为使商场的利润不低于2580元，则采购员采购的方案有哪几种？该商场最多可盈利__________元．
