题目内容
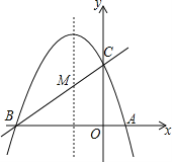
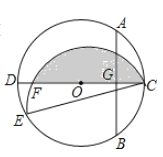
【题目】如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.点E为圆上一点,∠ECD=15°,将![]() 沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
【答案】![]()
【解析】
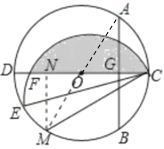
连接AO,将阴影部分沿CE翻折,点F的对应点为M,连接OM,过点M作MN⊥CD于点N,根据题意可以利用勾股定理求得⊙O的半径;得出S阴影=S弓形CBM,然后利用锐角三角函数、扇形的面积和三角形的面积即可解答本题.
解:连接AO,将阴影部分沿CE翻折,点F的对应点为M,如图所示,
∵CD为⊙O的直径,AB⊥CD,AB=8,
∴AG=![]() AB=4,
AB=4,
∵OG:OC=3:5,AB⊥CD,垂足为G,
∴设⊙O的半径为5k,则OG=3k,
∴(3k)2+42=(5k)2,
解得,k=1或k=1(舍去),
∴5k=5,
∴⊙O的半径是5;
将阴影部分沿CE翻折,点F的对应点为M,
∵∠ECD=15°,由对称性可知,∠DCM=30°,S阴影=S弓形CBM,
连接OM,则∠MOD=60°,
∴∠MOC=120°,
过点M作MN⊥CD于点N,
∴MN=MOsin60°=5×![]() =
=![]() ,
,
∴S阴影=S扇形OMCS△OMC=![]() =
=![]() ,
,
即图中阴影部分的面积是:![]() .
.
故答案为:![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目