题目内容
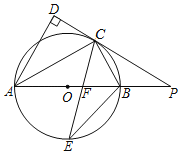
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() ,
,![]() .
.
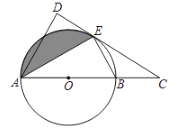
(1)求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)若![]() ,求出图中阴影部分的面积.
,求出图中阴影部分的面积.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)连接OE,证明△OBE为等边三角形,得到∠EOC=60°,根据切线的性质得到OE⊥CD,根据直角三角形的性质计算,得到答案;
(2)根据圆周角定理求出∠EAB=30°,得到EA=EC,根据含30°的直角三角形的性质计算,证明结论;
(3)求出∠AOE=120°,根据扇形面积公式、三角形的面积公式计算.
(1)解:连接OE.
∵OB=OE,∠ABE=60°,
∴△OBE为等边三角形,
∴∠EOC=60°.
∵CD与⊙O相切,
∴OE⊥CD,
∴∠C=90°﹣60°=30°;
(2)证明:由圆周角定理得,∠EAB=![]() ∠EOB=30°,
∠EOB=30°,
∴∠EAB=∠C,
∴EA=EC.
∵AD⊥CD,
∴∠DAC=90°﹣∠C=60°,
∴∠DAE=30°,
∴AE=2DE,
∴EC=2DE;
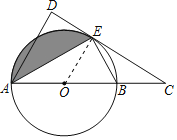
(3)解:∵∠EOC=60°,
∴∠AOE=120°,
则阴影部分的面积=扇形AOE的面积﹣△AOE的面积
=![]()
![]()
![]() ×
×![]() ×3×3×tan60°=
×3×3×tan60°=![]() .
.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目