题目内容
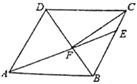
【题目】如图，在矩形
中，对角线
的垂直平分线
分别交
、、
于点
、
、
，连接
和
.
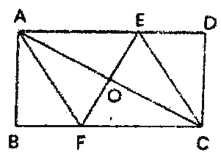
（1）求证：四边形
为菱形.
（2）若
，
，求菱形的周长.
【答案】（1）详见解析；（2）20
【解析】
（1）求出AO=OC，∠AOE=∠COF，根据平行线的性质得出∠EAO=∠FCO，根据ASA推出：△AEO≌△CFO；根据全等得出OE=OF，推出四边形是平行四边形，再根据EF⊥AC即可推出四边形是菱形；
（2）设菱形
的边长为
由题意得：
，
，
，再利用勾股定理进行计算即可解答.
（1）∵四边形
为矩形，
∴
，
∴
，
又∵
是
的垂直平分线，
∴
，
，
在
和
中，
，
∴
∴
∵，∴四边形为平行四边形.
∵
.∴四边形为菱形
（2）解：设菱形的边长为由题意得：，.
又∵
，
，∴，
∵四边形为矩形，
∴
，
在
中，由勾股定理得：
又∵
，，，
∴
，解得
.
∴菱形的周长=5×4=20
练习册系列答案
备战中考寒假系列答案
相关题目
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如下表：
碟子的个数 | 碟子的高度（单位：cm） |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |
（1）当桌子上放有x（个）碟子时，请写出此时碟子的高度（用含x的式子表示）；
（2）分别从三个方向上看，其三视图如上图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度．
