题目内容
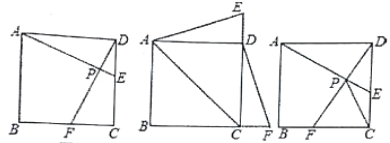
【题目】如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE，F为AE上一点，且∠BFE=∠C.
（1）求证： 
；
（2）若AB=4，∠BAE=30°，求AE的长.
【答案】(1)见解析；（2）
【解析】试题分析：（1）可通过证明∠BAF=∠AED，∠AFB=∠D，证得△ABF∽△EAD；
（2）先证出∠ABE=90°，再运用三角函数即可求出AE.
试题解析：（1）∵四边形ABCD是平行四边形
∴AD//BC，
∴∠C+∠ADE=180°
∵BFE=∠C，
∴∠AFB=∠EDA
又∵AB//DC
∴∠BAE=∠AED
∴
.
（2）∵AB//CD，BE⊥CD，
∴∠ABE=90°，
又∵AB=4，∠BAE=30°
设AE=x，则
由勾股定理得
解得
.
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
