题目内容
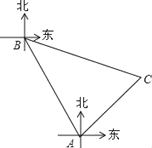
【题目】某海域有A、B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求:
(1)∠C= °;
(2)此时刻船与B港口之间的距离CB的长(结果保留根号).
【答案】(1)60;(2)![]()
【解析】(1)由平行线的性质以及方向角的定义得出∠FBA=∠EAB=30°,∠FBC=75°,那么∠ABC=45°,又根据方向角的定义得出∠BAC=∠BAE+∠CAE=75°,利用三角形内角和定理求出∠C=60°;
(2)作AD⊥BC交BC于点D,解Rt△ABD,得出BD=AD=30![]() ,解Rt△ACD,得出CD=10
,解Rt△ACD,得出CD=10![]() ,根据BC=BD+CD即可求解.
,根据BC=BD+CD即可求解.
解:(1)如图所示,
∵∠EAB=30°,AE∥BF,
∴∠FBA=30°,
又∠FBC=75°,
∴∠ABC=45°,
∵∠BAC=∠BAE+∠CAE=75°,
∴∠C=60°.
故答案为60;
(2)如图,作AD⊥BC于D,
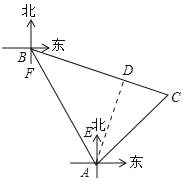
在Rt△ABD中,
∵∠ABD=45°,AB=60,
∴AD=BD=30![]() .
.
在Rt△ACD中,
∵∠C=60°,AD=30![]() ,
,
∴tanC=![]() ,
,
∴CD=![]() =10
=10![]() ,
,
∴BC=BD+CD=30![]() +10
+10![]() .
.
答:该船与B港口之间的距离CB的长为(30![]() +10
+10![]() )海里.
)海里.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目