题目内容
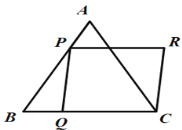
【题目】如图,等边△ABC边长为4,点P,Q分别是AB,BC边上的动点,且AP =BQ= x,作□PQCR,则用含x的代数式表示□PQCR的面积为______;当PC∥AR时, x =____.
【答案】![]() ;
; ![]() .
.
【解析】
过点P作PH⊥BC于点H,由AP=BQ=x得PB=QC=4-x,利用三角函数解Rt△BPH,得![]() ,进一步得到S与x的关系式.当PC∥AR时,证△AOR∽△ACOP,利用相似三角形对应边成比例列出方程求解即可.
,进一步得到S与x的关系式.当PC∥AR时,证△AOR∽△ACOP,利用相似三角形对应边成比例列出方程求解即可.
解:如图,过点P作PH⊥BC于点H,
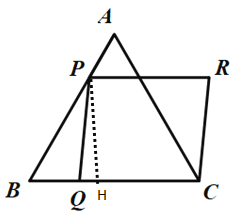
∴∠PHB=90°
∵等边三角形ABC
∴∠B=60°,BC=AB=4
∵AP=BQ=x,
∴PB=QC=4-x
在Rt△BPH中,∠B=60°
∴![]()
∴S平行四边形PQCR=QC·PH=![]() ;
;
当PC∥AR时,如图,连接PC,AR,AC、PR交于点O.
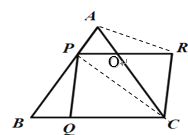
则△AOR∽△ACOP,
∴![]() =
=![]() ,
,
∵PR∥BC,
∴△APO是等边三角形,AO=AP=PO=x
∴OR=PR=PO=4-x-x=4-2x,CO=4-x
∴![]() =
=![]()
解得:x =![]()
∴当PC∥AR时, x =![]() .
.
故答案为:(1) ![]() ; (2)
; (2) ![]() .
.

练习册系列答案
相关题目