题目内容
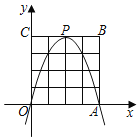
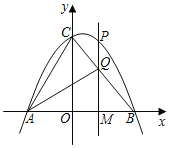
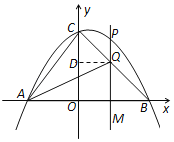
【题目】如图,抛物线y=﹣![]() x2+bx+c交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.
x2+bx+c交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.
(1)求此抛物线的表达式;
(2)求过B、C两点的直线的函数表达式;
(3)点P是第一象限内抛物线上的一个动点.过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点P的坐标,若不存在,请说明理由;
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)y=﹣x+4;(3)存在,(1,4)或(
x+4;(2)y=﹣x+4;(3)存在,(1,4)或(![]() ,
,![]() ).
).
【解析】
(1)将点A,B的坐标代入y=﹣![]() x2+bx+c即可;
x2+bx+c即可;
(2)先求出点C的坐标为(0,4),设直线BC的解析式为y=kx+4,再将点B(4,0)代入y=kx+4即可;
(3)先判断存在点P,求出AC,BC的长及∠OCB=∠OBC=45°,设点P坐标为(m,﹣![]() m2+
m2+![]() m+4),则点Q(m,﹣m+4),用含m的代数式表示出QM,AM的长,然后分①当AC=AQ时,②当AC=CQ时,③当CQ=AQ时三种情况进行讨论,列出关于m的方程,求出m的值,即可写出点P的坐标.
m+4),则点Q(m,﹣m+4),用含m的代数式表示出QM,AM的长,然后分①当AC=AQ时,②当AC=CQ时,③当CQ=AQ时三种情况进行讨论,列出关于m的方程,求出m的值,即可写出点P的坐标.
(1)将点A(﹣3,0),B(4,0)代入y=﹣![]() x2+bx+c,
x2+bx+c,
得,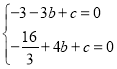 ,
,
解得,![]() ,
,
∴此抛物线的表达式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)在y=﹣![]() x2+
x2+![]() x+4中,
x+4中,
当x=0时,y=4,
∴C(0,4),
设直线BC的解析式为y=kx+4,
将点B(4,0)代入y=kx+4,
得,k=﹣1,
∴直线BC的解析式为y=﹣x+4;
(3)存在,理由如下:
∴A(﹣3,0),B(4,0),C(0,4),
∴OA=3,OC=OB=4,
∴AC=![]() =5,BC=
=5,BC=![]() =4
=4![]() ,∠OCB=∠OBC=45°,
,∠OCB=∠OBC=45°,
设点P坐标为(m,﹣![]() m2+
m2+![]() m+4),则点Q(m,﹣m+4),
m+4),则点Q(m,﹣m+4),
∴QM=﹣m+4,AM=m+3,
①当AC=AQ时,则AC=AQ=5,
(m+3)2+(﹣m+4)2=25,
解得:m1=1,m2=0(舍去),
当m=1时,﹣![]() m2+
m2+![]() m+4=4,
m+4=4,
则点P坐标为(1,4);
②当AC=CQ时,CQ=AC=5,
如图,过点Q作QD⊥y轴于点D,
则QD=CD=OM=m,
则有2m2=52,
解得m1=![]() ,m2=﹣
,m2=﹣![]() (舍去);
(舍去);
当m=![]() 时,﹣
时,﹣![]() m2+
m2+![]() m+4=
m+4=![]() ,
,
则点P坐标为(![]() ,
,![]() );
);
③当CQ=AQ时,(m+3)2+(﹣m+4)2=2m2,
解得:m=![]() (舍去);
(舍去);
故点P的坐标为(1,4)或(![]() ,
,![]() ).
).

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案