��Ŀ����
����Ŀ��������С��ͬѧ��Ƶ����������εĸ������ij߹���ͼ�Ĺ��̣�
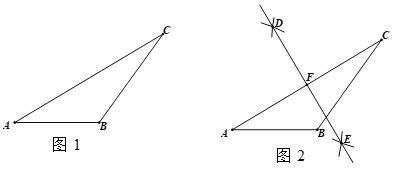
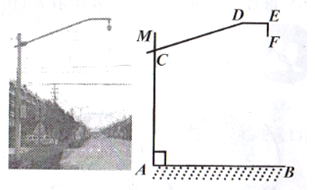
��֪����ͼ1����ABC��
������AB���ϵĸ��ߣ�
��������ͼ2��
�ٷֱ���A��CΪԲ�ģ�����![]() ��
��
Ϊ�뾶�����������ֱ��ڵ�D��E��
�� ��ֱ��DE����AC�ڵ�F��
�� �Ե�FΪԲ�ģ�FA��Ϊ�뾶��Բ����AB���ӳ����ڵ�M��
�� ����CM��
��CM Ϊ����AB���ϵĸ��ߣ�
����������ͼ���̣��ش����⣺
��1����ֱ�ߺ�Բ�棬��ȫͼ2�е�ͼ�Σ�
��2����������֤����
֤��������DA��DC��EA��EC��
������ͼ��֪DA=DC =EA=EC��
��DE���߶�AC�Ĵ�ֱƽ���ߣ�
��FA=FC ��
��AC�ǡ�F��ֱ����
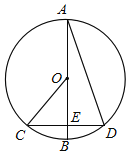
���AMC=______����___________________________________���������ݣ���
��CM��AB��
��CM����AB���ϵĸ��ߣ�
���𰸡���1����ͼ����������2��90��ֱ�����Ե�Բ�ܽ���ֱ��.
��������
��1������Ҫ������ͼ�μ��ɣ�
��2�������߶εĴ�ֱƽ���ߵ������Լ�Բ�ܽǶ���֤�����ɣ�
�⣺��1����ͼ�߶�AE��Ϊ����
��2������DA��DB��EA��EB��
��DA=DB��
���D���߶�AB�Ĵ�ֱƽ�����ϣ����߶����˾�����ȵĵ��������߶εĴ�ֱƽ�����ϣ���
��EA=EB��
���E���߶�AB�Ĵ�ֱƽ�����ϣ�
��DE���߶�AB�Ĵ�ֱƽ���ߣ�
��FA=FB��
��AB�ǡ�F��ֱ����
���AGB=90����ֱ�����Ե�Բ�ܽ���ֱ������
��AG��BC
��AG����BC���ϵĸ��ߣ�
�ʴ�Ϊ��90����ֱ�����Ե�Բ�ܽ���ֱ�ǣ�