��Ŀ����
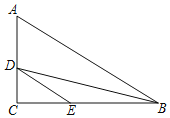
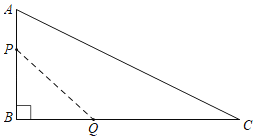
����Ŀ����ͼ��ʾ���ڡ�ABC�У���B��90�㣬AB��12mm��BC��24mm������P�ӵ�A��ʼ����2mm/S���ٶ��ر�AB��B�ƶ��������B�غϣ�������Q�ӵ�B��ʼ����4m/s���ٶ��ر�BC��C�ƶ�������C�غϣ������P��Q�ֱ��A��Bͬʱ���������˶���ʱ��Ϊxs���ı���APQC�����Ϊymm2��
��1��д��y��x֮��ĺ�������ʽ��
��2����x��2ʱ�����ı���APQC�������
���𰸡���1��y��4x2��24x+144����2��112mm2��
��������
��1����x��ʾPB��BQ����������ֱ�������ε��������ô𰸼��ɣ�
��2�����x��2ʱ��y��ֵ���ɵã�
�⣺��1�����˶�ʱ��Ϊx����P���ٶ�Ϊ2mm/s����Q���ٶ�Ϊ4mm/s��
��PB��12��2x��BQ��4x��
��y��![]() ��
��
��2����x��2ʱ��y��4��22��24��2+144��112��
����x��2ʱ���ı���APQC�����Ϊ112mm2��

��ϰ��ϵ�д�
�����Ŀ