题目内容
已知:二次函数y=a(x-1)2+4的图象如图所示,抛物线交y轴于点C,交x轴于A、B两点,用A点坐标为(-1,0).
(1)求a的值及点B的坐标.
(2)连接AC、BC,E是线段OC上的动点(不与O、C两点重合),过E点作直线PE⊥y轴交线段AC于点P,交线段BC于点Q.求证:
=
.
(3)设E点的坐标为(0,n),在线段AB上是否存在一点R,使得以P、Q、R为顶点的三角形与△B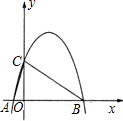 OC相似?若存在,求出n的值,并画出相应的示意图;若不存在,请说明理由.
OC相似?若存在,求出n的值,并画出相应的示意图;若不存在,请说明理由.
(1)求a的值及点B的坐标.
(2)连接AC、BC,E是线段OC上的动点(不与O、C两点重合),过E点作直线PE⊥y轴交线段AC于点P,交线段BC于点Q.求证:
| CE |
| CO |
| PQ |
| AB |
(3)设E点的坐标为(0,n),在线段AB上是否存在一点R,使得以P、Q、R为顶点的三角形与△B
 OC相似?若存在,求出n的值,并画出相应的示意图;若不存在,请说明理由.
OC相似?若存在,求出n的值,并画出相应的示意图;若不存在,请说明理由.(1)把A点坐标为(-1,0)代入y=a(x-1)2+4,得a(-1-1)2+4=0,解得a=-1,
∴y=-(x-1)2+4,
令y=0,-(x-1)2+4=0,
解得x1=-1,x2=3,
∴B点坐标为(3,0);
(2)证明:∵直线PE⊥y轴交线段AC于点P,交线段BC于点Q,
∴PQ∥AB,
∴△CPQ∽△CAB,
∴
=
;
(3)在线段AB上存在一点R,使得以P、Q、R为顶点的三角形与△BOC相似.理由如下
对于y=-(x-1)2+4,令x=0,y=3,
∴C点坐标为(0,3),
∴△OBC为等腰直角三角形,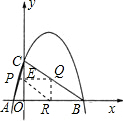
设直线BC的解析式为:y=kx+b,
把B(3,0),C(0,3)代入得,
,
解得k=-1,b=3,
∴直线BC的解析式为:y=-x+3;
同理可得直线AC的解析式为:y=-3x+3;
∵E点的坐标为(0,n),0<n<3,
∴P点坐标为(
-1,n),Q点的坐标为(3-n,n),
∴QP=3-n-(
-1)=4-
;
若以P、Q、R为顶点的三角形与△BOC相似,
∴以P、Q、R为顶点的三角形为等腰直角三角形,
当∠PQR=90°,QR=QP,如图,
∵PQ∥AB,
∴QR⊥AB,
∴QR=OE=n,
∴n=4-
,
解得n=
,
∴R的坐标为(
,0),
当∠QPR=90°,PQ=PR,同理可得n=
,得P点坐标为(-
,
),则R点坐标为(-
,0);
当∠PRQ=90°,RP=RQ,过R作RH⊥PQ于H,如图,
∴HR=
PQ,
∴n=
(4-
),
解得n=
,
∴P点的坐标为(-
,
),Q点的坐标为(
,
),
∴R点的坐标为(
,0).
所以当n=
,R的坐标为(
,0)或(-
,0);当n=
,R点的坐标为(
,0).
∴y=-(x-1)2+4,
令y=0,-(x-1)2+4=0,
解得x1=-1,x2=3,
∴B点坐标为(3,0);
(2)证明:∵直线PE⊥y轴交线段AC于点P,交线段BC于点Q,
∴PQ∥AB,
∴△CPQ∽△CAB,
∴
| CE |
| CO |
| PQ |
| AB |
(3)在线段AB上存在一点R,使得以P、Q、R为顶点的三角形与△BOC相似.理由如下
对于y=-(x-1)2+4,令x=0,y=3,
∴C点坐标为(0,3),
∴△OBC为等腰直角三角形,

设直线BC的解析式为:y=kx+b,
把B(3,0),C(0,3)代入得,
|
解得k=-1,b=3,
∴直线BC的解析式为:y=-x+3;
同理可得直线AC的解析式为:y=-3x+3;
∵E点的坐标为(0,n),0<n<3,
∴P点坐标为(
| n |
| 3 |
∴QP=3-n-(
| n |
| 3 |
| 4n |
| 3 |
若以P、Q、R为顶点的三角形与△BOC相似,
∴以P、Q、R为顶点的三角形为等腰直角三角形,
当∠PQR=90°,QR=QP,如图,
∵PQ∥AB,
∴QR⊥AB,
∴QR=OE=n,
∴n=4-
| 4n |
| 3 |
解得n=
| 12 |
| 7 |
∴R的坐标为(
| 9 |
| 7 |
当∠QPR=90°,PQ=PR,同理可得n=
| 12 |
| 7 |
| 3 |
| 7 |
| 12 |
| 7 |
| 3 |
| 7 |
当∠PRQ=90°,RP=RQ,过R作RH⊥PQ于H,如图,
∴HR=
| 1 |
| 2 |
∴n=
| 1 |
| 2 |
| 4n |
| 3 |
解得n=
| 6 |
| 5 |
∴P点的坐标为(-
| 3 |
| 5 |
| 6 |
| 5 |
| 9 |
| 5 |
| 6 |
| 5 |
∴R点的坐标为(
| 3 |
| 5 |
所以当n=
| 12 |
| 7 |
| 9 |
| 7 |
| 3 |
| 7 |
| 6 |
| 5 |
| 3 |
| 5 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 方向平移1个单位长度后得△AA1B1.
方向平移1个单位长度后得△AA1B1. A(m,0)、B(0,n).
A(m,0)、B(0,n).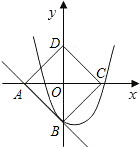 y=x2+bx+c经过点B且与直线AB只有一个公共点.
y=x2+bx+c经过点B且与直线AB只有一个公共点.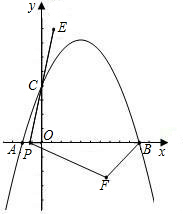 ,(0,2).
,(0,2).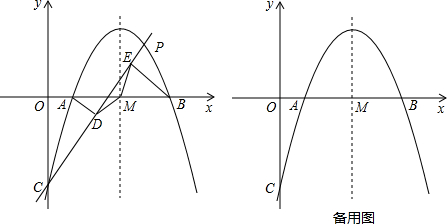
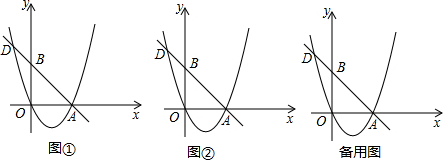
 A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.
A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.