题目内容
【题目】如图,矩形ABCD中,M、E、F三点在 ![]() 上,N是矩形两对角线的交点.若
上,N是矩形两对角线的交点.若 ![]() =24,
=24, ![]() =32,
=32, ![]() =16,
=16, ![]() =8,
=8, ![]() =7,则下列哪一条直线是A、C两点的对称轴?( )
=7,则下列哪一条直线是A、C两点的对称轴?( ) 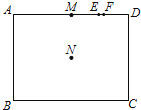
A.直线MN
B.直线EN
C.直线FN
D.直线DN
【答案】C
【解析】解:∵A、C两点的对称轴是线段AC的垂直平分线,
∴连接AC,过点N作AC的垂直平分线PN交AD于点P,
∵AB=24,AD=32,
∴ ![]() ,
,
∴AN=20,
∵∠PAN=∠CAD,∠ANP=∠ADC,
∴△ANP∽△ADC,
∴ ![]() ,即
,即 ![]() ,
,
解得,AP=25,
∵M、E、F三点在AD上,AD=32,MD=16,ED=8,FD=7,
∴AF=AD﹣FD=32﹣7=25,
∴点P与点F重合.
故选C.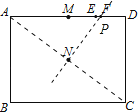
【考点精析】关于本题考查的矩形的性质和轴对称的性质,需要了解矩形的四个角都是直角,矩形的对角线相等;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目