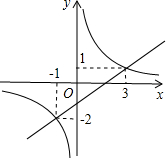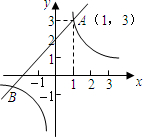题目内容
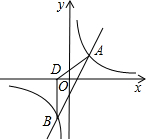
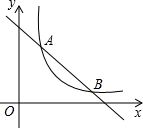
如图,已知反比例函数y=
与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的表达式;
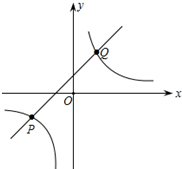
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
| k |
| x |
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

(1)∵已知反比例函数y=
经过点A(1,-k+4),
∴-k+4=
,即-k+4=k,
∴k=2,
∴A(1,2),
∵一次函数y=x+b的图象经过点A(1,2),
∴2=1+b,
∴b=1,
∴反比例函数的表达式为y=
.
一次函数的表达式为y=x+1.
(2)由
,
消去y,得x2+x-2=0.
即(x+2)(x-1)=0,
∴x=-2或x=1.
∴y=-1或y=2.
∴
或
.
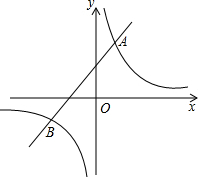
∵点B在第三象限,
∴点B的坐标为(-2,-1),
由图象可知,当反比例函数的值大于一次函数的值时,x的取值范围是x<-2或0<x<1.(10分)
| k |
| x |
∴-k+4=
| k |
| 1 |
∴k=2,
∴A(1,2),
∵一次函数y=x+b的图象经过点A(1,2),
∴2=1+b,
∴b=1,
∴反比例函数的表达式为y=
| 2 |
| x |
一次函数的表达式为y=x+1.
(2)由
|
消去y,得x2+x-2=0.
即(x+2)(x-1)=0,
∴x=-2或x=1.
∴y=-1或y=2.
∴
|
|
∵点B在第三象限,
∴点B的坐标为(-2,-1),
由图象可知,当反比例函数的值大于一次函数的值时,x的取值范围是x<-2或0<x<1.(10分)

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目