Question

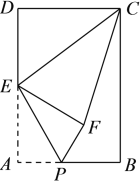
【题目】如图1，△ABC和△ADE中，AB=AC，AD=AE，且∠BAC=∠DAE．

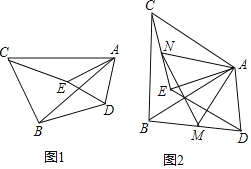
（1）求证：BD=CE；
（2）若点M，N分别是BD，CE的中点，如图2，连接AM，AN，MN，若AC=6，AE=4，∠EAC=60°，求AN的长．

Answer 1

【答案】（1）见解析；（2）．

【解析】

（1）由∠BAC=∠DAE知∠EAC=∠DAB，根据AB=AC、AD=AE即可证△CAE≌△BAD，从而得证；
（2）取AC的中点F，连接FN，过点N作NG⊥AC，据此可得NF∥AE、NF=AE=2，继而由∠GFN=∠EAC=60°得FG= FN=1、AG=4、NG=，利用勾股定理可得答案．

（1）∵∠BAC=∠DAE，
∴∠BAC-∠BAE=∠DAE-∠BAE，
∴∠EAC=∠DAB，
∵AB=AC、AD=AE，
∴△CAE≌△BAD，
∴BD=CE；
（2）取AC的中点F，连接FN，过点N作NG⊥AC于点G，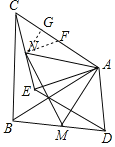

∵N是CE的中点，
∴NF∥AE，NF=AE=2，
∴∠GFN=∠EAC=60°，
∴∠FNG=30°，
∴FG=FN=1，
∴AG=1+3=4，NG=，
在Rt△ANG中，由勾股定理可得AN=．