题目内容
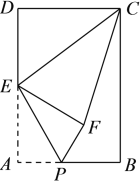
【题目】如图,在矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿EP折叠得到△EPF,连接CE,CF,当△ECF为直角三角形时,AP的长为______.
【答案】1或![]() .
.
【解析】
分∠CFE=90°和∠CEF=90°两种情况求AP得长即可.
①当∠CFE=90°时(如图所示),△ECF是直角三角形,
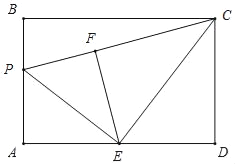
由折叠可得,∠PFE=∠A=90°,AE=FE=DE,
∴∠CFP=180°,即点P,F,C在一条直线上,
在Rt△CDE和Rt△CFE中,
![]() ,
,
∴Rt△CDE≌Rt△CFE(HL),
∴CF=CD=4,
设AP=FP=x,则BP=4﹣x,CP=x+4,
在Rt△BCP中,BP2+BC2=PC2,即(4﹣x)2+62=(x+4)2,
解得x=![]() ,即AP=
,即AP=![]() ;
;
②当∠CEF=90°时(如图所示),△ECF是直角三角形,
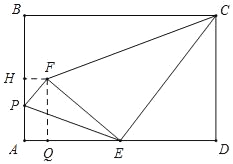
过F作FH⊥AB于H,作FQ⊥AD于Q,则∠FQE=∠D=90°,
又∵∠FEQ+∠CED=90°=∠ECD+∠CED,
∴∠FEQ=∠ECD,
∴△FEQ∽△ECD,
∴![]() ,即
,即![]() ,
,
解得FQ=![]() ,QE=
,QE=![]() ,
,
∴AQ=HF=![]() ,AH=
,AH=![]() ,
,
设AP=FP=x,则HP=![]() ﹣x,
﹣x,
∵Rt△PFH中,HP2+HF2=PF2,即(![]() ﹣x)2+(
﹣x)2+(![]() )2=x2,
)2=x2,
解得x=1,即AP=1.
综上所述,AP的长为1或![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?