题目内容
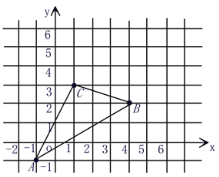
【题目】在平面直角坐标系中有三个点A(-3,2)、B(-4,-3)、C(-1,-1)
(1)连接A、B、C三点,请在右图中作出△ABC关于x轴对称的图形△A/B/C/,并直接写出对称点A/,B/,C/的坐标;
(2)用直尺在纵轴上找到一点P(0,n)满足PB/+PA的值最小(在图中标明点P的位置,并写出n的值在哪两个连续整数之间).
【答案】（1）图见详解，A’(-3,-2) B’(-4,3) C’(-1,1)
(2)点P的位置如图，n在2和3之间.
【解析】
（1）根据关于
轴对称的点的特征画出A,B,C三点的对应点，然后顺次连接即可. 关于轴对称的点的坐标满足：横坐标不变，纵坐标互为相反数.
（2）要想求
的最小值，就得想办法把它转化到一条直线上，可利用垂直平分线的性质作出A点关于
的对称点
，连接
，与轴的交点即P点.
（1）如图所示
A’(-3,-2) B’(-4,3) C’(-1,1)
（2）点P的位置如图，n在2和3之间.
练习册系列答案
相关题目
