题目内容
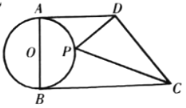
【题目】如图,在![]() 中
中![]() ,
,![]() ,
,![]() ,以
,以![]() 为直角边、
为直角边、![]() 为直角顶点作等腰直角三角形
为直角顶点作等腰直角三角形![]() ,则
,则![]() ______.
______.
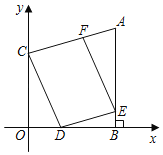
【答案】13
【解析】
由于AD=AB,∠CAD=90°,则可将△ABD绕点A逆时针旋转90°得△ABE,如图,根据旋转的性质得∠CAE=90°,AC=AE,BE=CD,于是可判断△ACE为等腰直角三角形,则∠ACE=45°,CE=![]() AC=5,易得∠BCE=90°,然后在Rt△CAE中利用勾股定理计算出BE=13,从而得到CD=13.
AC=5,易得∠BCE=90°,然后在Rt△CAE中利用勾股定理计算出BE=13,从而得到CD=13.
解:∵△ADB为等腰直角三角形,
∴AD=AB,∠BAD=90°,
将△ACD绕点A顺时针旋转90°得△AEB,如图,
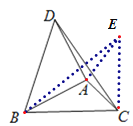
∴∠CAE=90°,AC=AE,CD=BE,
∴△ACE为等腰直角三角形,
∴∠ACE=45°,![]() ,
,
∵∠ACB=45°,
∴∠BCE=45°+45°=90°,
在Rt△BCE中,![]() ,
,
∴CD=13.
故答案为13.

练习册系列答案
相关题目