题目内容
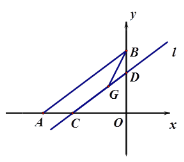
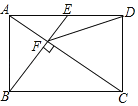
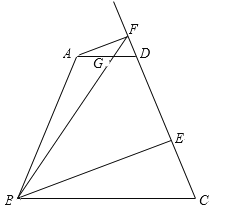
【题目】如图,在梯形ABCD中,AD // BC,AB = CD,AD = 5,BC = 15,![]() .E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,
.E为射线CD上任意一点,过点A作AF // BE,与射线CD相交于点F.联结BF,与直线AD相交于点G.设CE = x,![]() .
.
(1)求AB的长;
(2)当点G在线段AD上时,求y关于x的函数解析式,并写出函数的定义域;
(3)如果![]() ,求线段CE的长.
,求线段CE的长.
【答案】(1)AB = 13;(2)所求函数的解析式为![]() ,函数定义域为
,函数定义域为![]() ;(3)如果点G在边AD上,
;(3)如果点G在边AD上,![]() ;如果点G在边DA的延长线上,
;如果点G在边DA的延长线上,![]() .
.
【解析】
(1)分别过点A、D作AM⊥BC、DN⊥BC,垂足为点M、N,根据三角函数解答即可;
(2)根据相似三角形的判定和性质解答,进而利用函数解析式解答即可;
(3)根据两种情况,利用勾股定理解答即可.
解:(1)分别过点A、D作AM⊥BC、DN⊥BC,垂足为点M、N.
∵AD//BC,AB=CD,AD=5,BC=15,
∴![]() .
.
在Rt△ABM中,∠AMB=90°,
∴![]() .
.
∴AB=13.
(2)∵![]() ,∴
,∴![]() .即得
.即得![]() .
.
∵∠AFD=∠BEC,∠ADF=∠C.∴△ADF∽△BCE.
∴![]() .
.
又∵CE=x,![]() ,AB=CD=13.即得
,AB=CD=13.即得![]() .
.
∵AD//BC,∴![]() .∴
.∴ .
.
∴![]() .
.
∴所求函数的解析式为![]() ,函数定义域为
,函数定义域为![]() .
.
(3)在Rt△ABM中,利用勾股定理,得![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
设![]() .由△ADF∽△BCE,
.由△ADF∽△BCE,![]() ,得
,得![]() .
.
过点E作EH⊥BC,垂足为点H.
由题意,本题有两种情况:
(ⅰ)如果点G在边AD上,则![]() .
.
∴S=5.
∴![]() .
.
∴![]() .
.
∴![]() .
.
由DN⊥BC,EH⊥BC,易得EH//DN.
∴![]() .
.
又CD=AB=13,∴![]() .
.
(2)如果点G在边DA的延长线上,则![]() .
.
∴![]() .解得
.解得![]() .
.
∴![]() .
.
∴![]() .解得
.解得![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目