Question

【题目】如图，一张半径为的圆形纸片，点为圆心，将该圆形纸片沿直线折叠，直线交于两点．

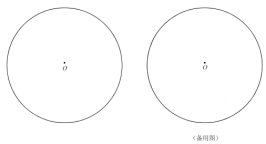
（1）若折叠后的圆弧恰好经过点，利用直尺和圆规在图中作出满足条件的一条直线（不写作法，保留作图痕迹），并求此时线段的长度．

（2）已知是一点，．

①若折叠后的圆弧经过点，则线段长度的取值范围是________．

②若折叠后的圆弧与直线相切于点，则线段的长度为_________．

Answer 1

【答案】（1）图见解析，；（2）①；②

【解析】

（1）连接AO，直线l垂直平分PO．，在Rt△AHO中即可求解；

（2）①分两种情况求解；

②过O作弦AB的垂直与圆交于点D，与弧AB交于点C，与AB交于点E，过M作OM的垂线，两条垂线的交点为O'，连接AO，得到OO'垂直平分AB，O'为弧ABM所在圆的圆心，，在Rt△ADO中即可求解；

（1）如图，直线为所求，连接．

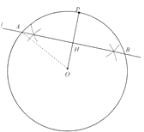
∵点与点关于直线对称，

∴直线垂直平分．

∴．

在中，

∵，

∴．

在中，

∵，为半径，

∴．

（2）如图1：

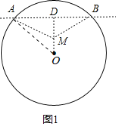
∵弧AB翻折与M重合，OM=1，

∴DM=1，

在Rt△ADO中，AO=3，DO=2，

∴；

如图2：

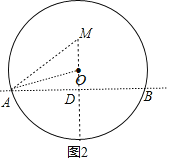
∵弧AB翻折与M重合，OM=1，

∴MD=2，DO=1，

在Rt△ADO中，AO=3，

∴，

∴，

故答案为；

（3）如图3：过O作弦AB的垂线与圆O交于点C，与AB交于点D，连接OM，过点M作OM的垂线，两条垂线的交点为O'，连接AO，

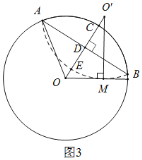
∴OO'垂直平分AB，O'为弧ABM所在圆的圆心，

∵折叠后的圆弧与直线OM相切于点M，

∴MO'=3，CO=EO'，在Rt△OO'M中，OM=1，

∴，

在Rt△ADO中，，AO=3，

∴，

∴；

故答案为