题目内容
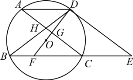
【题目】如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及其延长线分别交AC,BC于点G,F.
(1)求证:DF垂直平分AC;
(2)若弦AD=10,AC=16,求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径为![]() .
.
【解析】
(1)根据“切线的性质和垂径定理”进行分析证明即可;
(2)如下图,连接AO,由垂径定理可得AG=![]() AC=8,这样在Rt△ADG中由勾股定理可得GD=6,设⊙O的半径为r,则OG=r-6,由此在Rt△AOG中由勾股定理建立关于r的方程,解方程即可求得r的值.
AC=8,这样在Rt△ADG中由勾股定理可得GD=6,设⊙O的半径为r,则OG=r-6,由此在Rt△AOG中由勾股定理建立关于r的方程,解方程即可求得r的值.
(1)∵DE是⊙O的切线,且DF过圆心O,
∴DF⊥DE.
又∵AC∥DE,∴DF垂直平分AC.
(2)如下图,连接AO,

∵AG=GC,AC=16,
∴AG=8.
∴在Rt△AGD中,GD=![]() ,
,
设⊙O的半径为r,则OG=r-6,
∵ 在Rt△AOG中,![]() ,
,
∴![]() .
.
解得r=![]() .即⊙O的半径为
.即⊙O的半径为![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目