题目内容
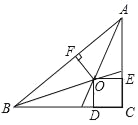
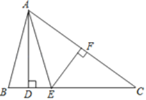
【题目】如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:
(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;
(乙)作过B点且与AB垂直的直线l,作过C点且与AC垂直的直线,交l于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述何者正确?( )
A. 两人皆正确 B. 两人皆错误
C. 甲正确,乙错误 D. 甲错误,乙正确
【答案】D
【解析】甲:根据作图可得AC=AP,利用等边对等角得:∠APC=∠ACP,由平角的定义可知:∠BPC+∠APC=180°,根据等量代换可作判断;
乙:根据四边形的内角和可得:∠BPC+∠A=180°.
甲:如图1,

∵AC=AP,
∴∠APC=∠ACP,
∵∠BPC+∠APC=180°
∴∠BPC+∠ACP=180°,
∴甲错误;
乙:如图2,
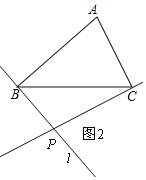
∵AB⊥PB,AC⊥PC,
∴∠ABP=∠ACP=90°,
∴∠BPC+∠A=180°,
∴乙正确,
故选:D.

练习册系列答案
相关题目
【题目】已知甲、乙两袋中各装有若干颗球,其种类与数量如表所示.今阿冯打算从甲袋中抽出一颗球,小潘打算从乙袋中抽出一颗球,若甲袋中每颗球被抽出的机会相等,且乙袋中每颗球被抽出的机会相等,则下列叙述何者正确?( )
甲袋 | 乙袋 | |
红球 | 2颗 | 4颗 |
黄球 | 2颗 | 2颗 |
绿球 | 1颗 | 4颗 |
总计 | 5颗 | 10颗 |
A. 阿冯抽出红球的机率比小潘抽出红球的机率大
B. 阿冯抽出红球的机率比小潘抽出红球的机率小
C. 阿冯抽出黄球的机率比小潘抽出黄球的机率大
D. 阿冯抽出黄球的机率比小潘抽出黄球的机率小