Question

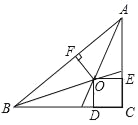
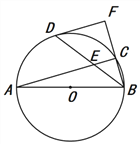
【题目】已知：如图，△ABC内接于⊙O，AB为直径，点D是弧AC的中点，连结BD交AC于点E，过D点作⊙O的切线交BC的延长线于F．

（1）求证：∠FDB = ∠AED.

（2）若⊙O 的半径为5，tan∠FBD＝，求CF的长．

Answer 1

【答案】(1)见解析;(2) .

【解析】（1） 连结OD，交弦AC于点G.证明DFAC，即可得到∠FDB=∠AED，

(2)连结AD 根据圆周角定理可得∠FBD=∠ABD=∠DAC, tan∠FBD=tan∠ABD=tan∠DAC= , 在中，AB=2×5=10, tan∠ABD=,设AD=3x,则BD=4x，根据勾股定理列出方程 解得x=2, 在中，AD=6, tan∠DAC=

同理可得：DG = ,证明CF=DG，即可求解.

（1） 连结OD，交弦AC于点G.

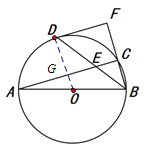
∵ DF切⊙O于点D，

∴ OD⊥DF，

∵ 点D是弧AC的中点，

∴ OD⊥AC，

∴ DFAC，

∴∠FDB=∠AED，

(2)连结AD

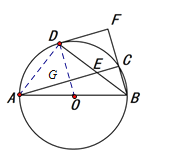
∵点D是弧AC的中点

∴ 弧AD=弧CD∴ ∠FBD=∠ABD=∠DAC,

∴ tan∠FBD=tan∠ABD=tan∠DAC= ,

在中，AB=2×5=10, tan∠ABD=,

设AD=3x,则BD=4x∴

解得x=2,

∴ AD=6,

在中，AD=6, tan∠DAC=

同理可得：DG =

∵ AB是直径∴ ∠ACF=∠ACB=90°

∵ ∠FDO=∠DGC=90°∴ 四边形DGCF是矩形

∴ CF=DG=.