题目内容
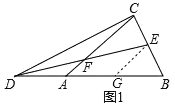
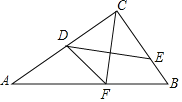
【题目】如图，△ABC中，AB＝AC，点D在BA的延长线上，点E在BC上，DE＝DC，点F是DE与AC的交点.
（1）求证：∠BDE＝∠ACD
（2）若DE＝2DF，过点E作EG∥AC交AB于点G，求证：AB＝2AG；
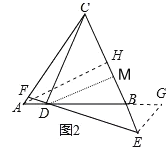
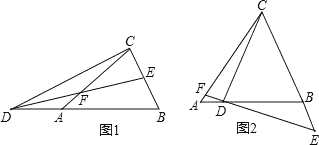
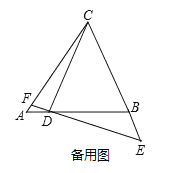
（3）将“点D在BA的延长线上，点E在BC上” 改为“点D在AB上，点E在CB的延长线上”，“点F是DE与AC的交点改为 “点F是ED的延长线与AC的交点”，其它条件不变，如图.
① 求证：
；
② 若DE＝4DF，请直接写出S△ABC∶S△DEC的值.
【答案】（1）见解析； （2）见解析； （3）① 见解析；② 
.
【解析】
（1）运用等腰三角形的性质及三角形的外角性质就可解决问题；
（2）过点E作EG∥AC，交AB于点G，如图1，证明△DCA≌△EDG，可得DA＝EG ，CA＝DG，再由DF＝EF，得到DA＝AG＝BG；
（3）①过点E作EG∥AC，交AB的延长线于点G，如图2，证明△DCA≌△EDG，可得AD=GE，由AC∥EG得△ABC∽△GBE，BG=GE，根据相似三角形对应边成比例列式可得结果；②作AH垂直BC于H，作DM⊥CE于M，由△ADF∽△CDE及AD= GE= BG可得
，由△ABC∽△GBE可得
，根据三角形面积公式列出比例式化简即可.
解：（1）证明：∵AB＝AC，DC＝DE，
∴∠ABC＝∠ACB，∠DEC＝∠DCE．
∴∠BDE＝∠DEC∠DBC＝∠DCE∠ACB＝∠ACD．
（2）过点E作EG∥AC，交AB于点G，如图1，
则有∠DAC＝∠DGE．
在△DCA和△EDG中，
∠DCA＝∠GDE，
∠DAC＝∠DGE，
DC＝DE，
∴△DCA≌△EDG（AAS）．
∴DA＝EG，CA＝DG，
∴DG＝AB．
∴DA＝BG．
∵AF∥EG，DF＝EF，
∴DA＝AG．
∴AG＝BG．
∴AB＝2AG．
（3）①过点E作EG∥AC，交AB的延长线于点G，如图2，
∵AB＝AC，DC＝DE，
∴∠ABC＝∠ACB，∠DEC＝∠DCE．
∴∠BDE＝∠DBC∠DEC＝∠ACB∠DCE＝∠DCA．
∵AC∥EG，
∴∠DAC＝∠DGE．
在△DCA和△EDG中，
，
∴△DCA≌△EDG（AAS），
∴AD=GE，
∵AC∥EG，
∴△ABC∽△GBE，AB=AC，
∴BG=GE，
∴
，
∴
即：
；
②∵AC∥EG，
∴△ADF∽△CDE，
∴
，
∵AD= GE= BG，
∴
，
作AH垂直BC于H，作DM⊥CE于M，如图2，
∴AH∥DM，
∴
，
又∵△ABC∽△GBE，
∴
，
∴，
∴
.
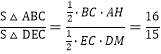黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
