ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() СНЕу(Еу
СНЕу(Еу![]() дкЕу
дкЕу![]() ЕФзѓВр)ЃЌгы
ЕФзѓВр)ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() СЌНг
СЌНг![]() Еу
Еу![]() ЪЧЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕу
ЪЧЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊЕу
жсЃЌДЙзуЮЊЕу![]() НЛ
НЛ![]() гкЕу
гкЕу![]() Й§Еу
Й§Еу![]() зї
зї![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
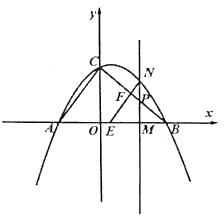
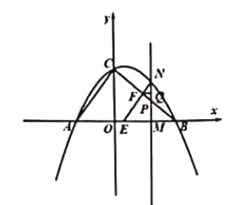
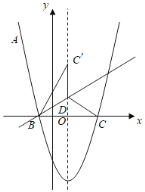
ЃЈ1ЃЉЧѓ![]() Ш§ЕуЕФзјБъЃЛ
Ш§ЕуЕФзјБъЃЛ
ЃЈ2ЃЉЪдЬНОПдкЕу![]() дЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкетбљЕФЕу
дЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкетбљЕФЕу![]() ЪЙЕУвдЕу
ЪЙЕУвдЕу![]() ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌШєДцдкЃЌЧыЧѓГіДЫЪБЕу
ЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌШєДцдкЃЌЧыЧѓГіДЫЪБЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉmЪЧЕу![]() ЕФКсзјБъЃЌЧыгУКЌ
ЕФКсзјБъЃЌЧыгУКЌ![]() ЕФДњЪ§ЪНБэЪОЯпЖЮ
ЕФДњЪ§ЪНБэЪОЯпЖЮ![]() ЕФГЄЃЌВЂЧѓГі
ЕФГЄЃЌВЂЧѓГі![]() ЮЊКЮжЕЪБ
ЮЊКЮжЕЪБ![]() газюДѓжЕЃЎ
газюДѓжЕЃЎ
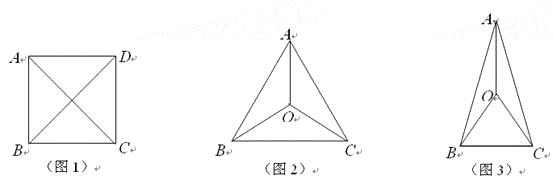
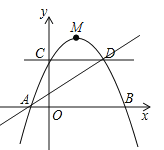
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉДцдкТњзуЬѕМўЕФЕу
ЃЛЃЈ2ЃЉДцдкТњзуЬѕМўЕФЕу![]() зјБъЮЊ
зјБъЮЊ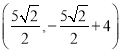 КЭ
КЭ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕЃЎ
газюДѓжЕЃЎ
ЁОНтЮіЁП
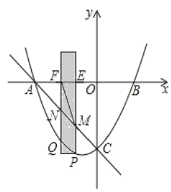
ЃЈ1ЃЉНтЗНГЬ![]() ЕУ
ЕУ![]() ЃЌМЦЫуздБфСПЮЊ0ЪБЕФЖўДЮКЏЪ§жЕЕУCЕузјБъЃЛ
ЃЌМЦЫуздБфСПЮЊ0ЪБЕФЖўДЮКЏЪ§жЕЕУCЕузјБъЃЛ
ЃЈ2ЃЉРћгУЙДЙЩЖЈРэМЦЫуГі![]() ЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУжБЯп
ЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУжБЯп![]() ЙиЯЕЪНЮЊ
ЙиЯЕЪНЮЊ![]() дђПЩЩш
дђПЩЩш![]() ЮЊ
ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЬжТлЃКЕБ
ЃЌЬжТлЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌга
ЪБЃЌга![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌга
ЪБЃЌга![]() ШЛКѓЗжБ№НтЗНГЬЧѓГі
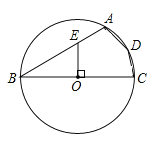
ШЛКѓЗжБ№НтЗНГЬЧѓГі![]() МДПЩЕУЕНЖдгІЕуPЕФзјБъЃЛ
МДПЩЕУЕНЖдгІЕуPЕФзјБъЃЛ
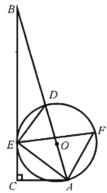
ЃЈ3ЃЉЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌгЩ
ЃЌгЩ![]() жЊ
жЊ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌПЩХаЖЯ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌПЩХаЖЯ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌдђ
ЮЊЕШбќжБНЧШ§НЧаЮЃЌдђ![]() дйжЄУї
дйжЄУї![]() ЕУЕН
ЕУЕН![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌгкЪЧЕУЕН
ЃЌгкЪЧЕУЕН![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() РћгУ
РћгУ![]() ЕУЕН
ЕУЕН![]() ЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтМДПЩЃЎ
ЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтМДПЩЃЎ
НтЃК![]() ЕБ
ЕБ![]() ЪБЃЌга
ЪБЃЌга![]()
НтЕУ![]() ЃЌ
ЃЌ
Ыљвд![]()
ЕБ![]() ЪБЃЌга
ЪБЃЌга![]()
Ыљвд![]() ЃЎ
ЃЎ
![]() ДцдкЃЎ
ДцдкЃЎ
гЩЃЈ1ЃЉвзжЊЃЌ![]() ЃЌ
ЃЌ
жБЯп![]() ЙиЯЕЪНЮЊ
ЙиЯЕЪНЮЊ![]()
Щш![]() ЮЊ
ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђЂйЕБ![]() ЪБЃЌ
ЪБЃЌ
га![]()
НтЕУ![]() (ВЛКЯЃЌЩсШЅ)ЃЌ
(ВЛКЯЃЌЩсШЅ)ЃЌ
ДЫЪБ![]() ЕуЮЊ
ЕуЮЊ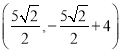
ЂкЕБ![]() ЪБЃЌга
ЪБЃЌга![]()
НтЕУ![]() (ВЛКЯЃЌЩсШЅ)ЃЌ
(ВЛКЯЃЌЩсШЅ)ЃЌ
ДЫЪБ![]() ЕуЮЊ
ЕуЮЊ![]()
ЂлЕБ![]() ЪБЃЌга
ЪБЃЌга![]()
НтЕУ![]() (ВЛКЯЃЌЩсШЅ)ЃЌ
(ВЛКЯЃЌЩсШЅ)ЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕу![]() зјБъЮЊ
зјБъЮЊ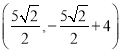 КЭ
КЭ![]() ЃЎ
ЃЎ
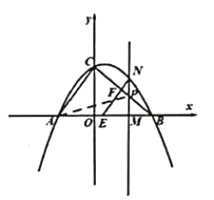
![]() Й§Еу
Й§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌШчЭМЃЌ
ЃЌШчЭМЃЌ
дђ![]() жсЃЌ
жсЃЌ
гЩ![]() жЊ
жЊ![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
![]() ЃЌ
ЃЌ
![]() ЮЊЕШбќжБНЧШ§НЧаЮ
ЮЊЕШбќжБНЧШ§НЧаЮ
![]()
![]() ЃЌ
ЃЌ
![]()
гж![]() ЃЌ
ЃЌ
![]()
![]()
МД![]()
![]()
![]()
![]() ЃЌ
ЃЌ
Щш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
дђ![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]() газюДѓжЕЃЌ
газюДѓжЕЃЌ
![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕЃЎ
газюДѓжЕЃЎ