题目内容
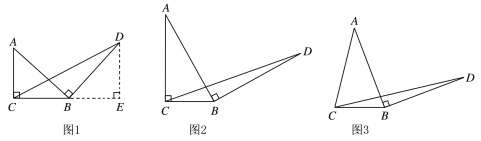
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.

【答案】3或![]()
【解析】
△AB′F为直角三角形,应分两种情况进行讨论.当∠AFB′为直角时,利用勾股定理求出B′E,也就是BE的长,便求出AE。当∠AB′F为直角时,过A作AN⊥EB′,交EB′的延长线于N,构造Rt△B′EF,利用勾股定理便可求出AE.
解:①当B′D⊥AE时,△AB′F为直角三角形,如下图:
根据题意,BE=B′E,BD= B′D=![]() BC=
BC=![]() . ∠B=∠EB′F
. ∠B=∠EB′F
∵在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2
,AC=2
∴AB=![]() =
=![]() =4
=4
∴∠B=∠EB′F =30°.
∵在Rt△BDF中,∠B=30°
∴DF=![]() BD=
BD=![]()
∴B′F=B′D-DF=![]() -
-![]() =
=![]()
∵在Rt△B′EF中,∠EB′F =30°
∴EF=![]() B′E,
B′E,
∵B′F=![]() =
=![]() =
=![]() EF,
EF,
即![]() =
=![]() EF,
EF,
∴EF=![]() ,则BE=1,
,则BE=1,
∴AE=AB-BE=4-1=3.
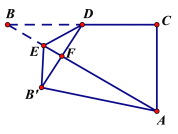
②当D B′⊥A B′时,△AB′F为直角三角形,如下图:

连接AD,过A作AN⊥EB′,交EB′的延长线于N.
根据题意,BE=B′E,BD=CD=B′D=![]() BC=
BC=![]() . ∠B=∠EB′F
. ∠B=∠EB′F
∵在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2
,AC=2
∴AB=![]() =
=![]() =4
=4
∴∠B=∠EB′F =30°.
∵∠AB′F=90°
∴∠AB′E=∠AB′F+∠EB′F=120°
∴Rt△AB′N中,∠AB′N=60°,∠B′AN=30°
∴B′N=![]() AB′
AB′
在Rt△AB′D和Rt△ACD中
![]()
∴Rt△AB′D≌Rt△ACD(HL)
∴AB′=AC=2
∴B′N=1,AN=![]()
设AE=x,则BE= B′E=4-x
∵在Rt△AEN中,![]()
∴(![]() )2+(4-x+1)2=x2
)2+(4-x+1)2=x2
∴x=![]()
综上,AE的长为3或![]() .
.

【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有3,4,5,x,甲,乙两人每次同时从袋中各随机取出1个小球,并计算2个小球上的数字之和.记录后将小球放回袋中搅匀,进行重复试验,试验数据如下表:
摸球总 次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出 现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出 现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果试验继续进行下去,根据上表提供的数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是________;
(2)如果摸出的2个小球上数字之和为9的概率是,那么x的值可以为7吗?为什么?